
【题目】已知点![]() ,直线
,直线![]() :
:![]() ,点
,点![]() 为
为![]() 上一动点,过
上一动点,过![]() 作直线
作直线![]() ,
,![]() 为
为![]() 的中垂线,
的中垂线,![]() 与
与![]() 交于点
交于点![]() ,设点
,设点![]() 的轨迹为曲线Γ.
的轨迹为曲线Γ.
(1)求曲线Γ的方程;
(2)若过![]() 的直线与Γ交于
的直线与Γ交于![]() 两点,线段
两点,线段![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() ,求
,求![]() 与
与![]() 的比值.
的比值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】为了解某地网民浏览购物网站的情况,从该地随机抽取100名网民进行调查,其中男性、女性人数分别为60和40.下面是根据调查结果统计的数据,将日均浏览购物网站时间不低于40分钟的网民称为“网购达人”,已知“网购达人”中女性人数为15人.
日均浏览购物网站时间(分钟) |
|
|
|
|
|
|
人数 | 2 | 14 | 24 | 35 | 20 | 5 |
(1)根据已知条件完成下面的![]() 列联表,并判断是否有99%的把握认为是否为“网购达人”与性别有关;
列联表,并判断是否有99%的把握认为是否为“网购达人”与性别有关;
非网购达人 | 网购达人 | 总计 | |
男 | |||
女 | 15 | ||
总计 |
(2)从上述调查中的“网购达人”中按性别分层抽样,抽取5人发放礼品,再从这5人中随机选出2人作为“最美网购达人”,求这两个“最美网购达人”中恰好为1男1女的概率.
参考公式: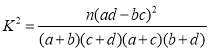 ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校拟从甲、乙两名同学中选一人参加疫情知识问答竞赛,于是抽取了甲、乙两人最近同时参加校内竞赛的十次成绩,将统计情况绘制成如图所示的折线图.根据该折线图,下面结论正确的是( )
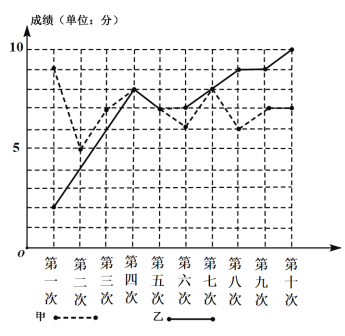
A.甲、乙成绩的中位数均为7
B.乙的成绩的平均分为6.8
C.甲从第四次到第六次成绩的下降速率要大于乙从第四次到第五次的下降速率
D.甲的成绩的方差小于乙的成绩的方差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 的底面是等边三角形,
的底面是等边三角形,![]() 在底面ABC上的射影为
在底面ABC上的射影为![]() 的重心G.
的重心G.
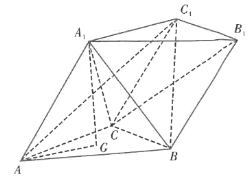
(1)已知![]() ,证明:平面
,证明:平面![]() 平面
平面![]() ;
;
(2)若三棱柱![]() 的侧棱与底面所成角的正切值为
的侧棱与底面所成角的正切值为![]() ,
,![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
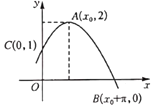
【题目】已知函数![]() 的部分图象如图所示,若将函数
的部分图象如图所示,若将函数![]() 的图象纵坐标不变,横坐标缩短到原来的
的图象纵坐标不变,横坐标缩短到原来的![]() ,再向右平移
,再向右平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,则下列命题正确的是( ).
的图象,则下列命题正确的是( ).
A.函数![]() 的解析式为
的解析式为![]()
B.函数![]() 的解析式为
的解析式为![]()
C.函数![]() 图象的一条对称轴是直线
图象的一条对称轴是直线![]()
D.函数![]() 在区间
在区间![]() 上单调递增
上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() 、
、![]() .
.
(1)若![]() ,且函数
,且函数![]() 的图象是函数
的图象是函数![]() 图象的一条切线,求实数
图象的一条切线,求实数![]() 的值;
的值;
(2)若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若对任意实数![]() ,函数
,函数![]() 在
在![]() 上总有零点,求实数
上总有零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某病毒研究所为了更好地研究“新冠”病毒,计划改建十个实验室,每个实验室的改建费用分为装修费和设备费,每个实验室的装修费都一样,设备费从第一到第十实验室依次构成等比数列,已知第五实验室比第二实验室的改建费用高42万元,第七实验室比第四实验室的改建费用高168万元,并要求每个实验室改建费用不能超过1700万元.则该研究所改建这十个实验室投入的总费用最多需要( )
A.3233万元B.4706万元C.4709万元D.4808万元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com