
【题目】已知函数![]() .
.
(1)当a=1时,讨论f(x)的单调性;
(2)当x≥0时,f(x)≥![]() x3+1,求a的取值范围.
x3+1,求a的取值范围.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 是曲线
是曲线![]() 与
与![]() 的交点,点
的交点,点![]() 是曲线
是曲线![]() 与
与![]() 的交点,
的交点,![]() 、
、![]() 均异于原点
均异于原点![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)利用“五点法”画出函数![]() 在长度为一个周期的闭区间的简图.
在长度为一个周期的闭区间的简图.
列表:
| |||||
x | |||||
y |
作图:
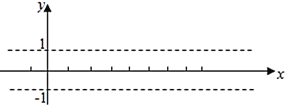
(2)并说明该函数图象可由![]() 的图象经过怎么变换得到的.
的图象经过怎么变换得到的.
(3)求函数![]() 图象的对称轴方程.
图象的对称轴方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B分别为椭圆E:![]() (a>1)的左、右顶点,G为E的上顶点,
(a>1)的左、右顶点,G为E的上顶点,![]() ,P为直线x=6上的动点,PA与E的另一交点为C,PB与E的另一交点为D.
,P为直线x=6上的动点,PA与E的另一交点为C,PB与E的另一交点为D.
(1)求E的方程;
(2)证明:直线CD过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱柱ABC–A1B1C1的底面是正三角形,侧面BB1C1C是矩形,M,N分别为BC,B1C1的中点,P为AM上一点.过B1C1和P的平面交AB于E,交AC于F.
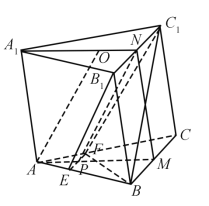
(1)证明:AA1//MN,且平面A1AMN⊥平面EB1C1F;
(2)设O为△A1B1C1的中心,若AO=AB=6,AO//平面EB1C1F,且∠MPN=![]() ,求四棱锥B–EB1C1F的体积.
,求四棱锥B–EB1C1F的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2xsin2x.
(1)讨论f(x)在区间(0,π)的单调性;
(2)证明:![]() ;
;
(3)设n∈N*,证明:sin2xsin22xsin24x…sin22nx≤![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
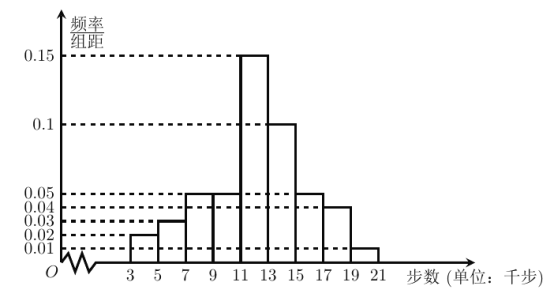
【题目】随着智能手机的普及,手机计步软件迅速流行开来,这类软件能自动记载每个人每日健步的步数,从而为科学健身提供一定的帮助.某市工会为了解该市市民每日健步走的情况,从本市市民中随机抽取了2000名市民(其中不超过40岁的市民恰好有1000名),利用手机计步软件统计了他们某天健步的步数,并将样本数据分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 九组(单位;千步),将抽取的不超过40岁的市民的样本数据绘制成频率分布直方图如图,将40岁以上的市民的样本数据绘制成频数分布表如下,并利用该样本的频率分布估计总体的概率分布.
九组(单位;千步),将抽取的不超过40岁的市民的样本数据绘制成频率分布直方图如图,将40岁以上的市民的样本数据绘制成频数分布表如下,并利用该样本的频率分布估计总体的概率分布.
分组(单位 千步) |
|
|
|
|
|
|
|
|
|
频数 | 10 | 20 | 20 | 30 | 400 | 200 | 200 | 100 | 20 |
(1)现规定,日健步步数不低于13000步的为“健步达人”,填写下面列联表,并根据列联表判断能否有99.9%的把握认为是否为“健步达人”与年龄有关;
健步达人 | 非健步达人 | 总计 | |
40岁以上的市民 | |||
不超过40岁的市民 | |||
总计 |
(2)利用样本平均数和中位数估计该市不超过40岁的市民日健步步数(单位:千步)的平均数和中位数;
(3)若日健步步数落在区间![]() 内,则可认为该市民”运动适量”,其中
内,则可认为该市民”运动适量”,其中![]() ,
,![]() 分别为样本平均数和样本标准差,计算可求得频率分布直方图中数据的标准差
分别为样本平均数和样本标准差,计算可求得频率分布直方图中数据的标准差![]() 约为3.64.若一市民某天的健步步数为2万步,试判断该市民这天是否“运动适量”?
约为3.64.若一市民某天的健步步数为2万步,试判断该市民这天是否“运动适量”?
参考公式: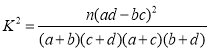
![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com