
【题目】某中学在全校范围内举办了一场“中国诗词大会”的比赛,规定初赛测试成绩不小于160分的学生进入决赛阶段比赛.现有200名学生参加测试,并将所有测试成绩统计如下表:
分数段 | 频数 | 频率 |
| 6 | 0.03 |
|
| 0.38 |
| 100 | 0.5 |
|
|
|
| 6 | 0.03 |
合计 | 200 | 1 |
(1)计算![]() 的值;
的值;
(2)现利用分层抽样的方法从进入决赛的学生中选择6人,再从选出的6人中选2人做进一步的研究,求选择的2人中至少有1人的分数在![]() 的概率.
的概率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由频率和为1,求出![]() ,从而求出
,从而求出![]() ,再由频数和为200,求出
,再由频数和为200,求出![]() ;
;
(2)按比例求出两组抽取的人数,并把6人编号,所求事件的概率为古典概型的概率,列出6人中选2人的所有情况,找出至少有1人的分数在![]() 的选法, 即可求出概率
的选法, 即可求出概率
(1)![]() ,
,
![]() ,
,
![]() ;
;
(2)利用分层抽样的方法从进入决赛的学生中选择6人,
则![]() 组中选4人,记为1,2,3,4;
组中选4人,记为1,2,3,4;
![]() 组选2人,记为A,B. 从选出的6人中选2人
组选2人,记为A,B. 从选出的6人中选2人
所有情况有:{1,2},{1,3},{1,4},{1,A},{1,B},{2,3},{2,4},
{2,A},{2,B},{3,4},{3,A},{3,B},{4,A},{4,B},{A,B}.共有15
种选法,选择的2人中至少有1人的分数在![]() 有9种选法.
有9种选法.
![]() 选择的2人中至少有1人的分数在
选择的2人中至少有1人的分数在![]() 的概率为
的概率为![]() .
.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】地球海洋面积远远大于陆地面积,随着社会的发展,科技的进步,人类发现海洋不仅拥有巨大的经济利益,还拥有着深远的政治利益.联合国于第63届联合国大会上将每年的6月8日确定为“世界海洋日”.2019年6月8日,某大学的行政主管部门从该大学随机抽取100名大学生进行一次海洋知识测试,并按测试成绩(单位:分)分组如下:第一组![]() ,第二组
,第二组![]() ,第二组
,第二组![]() ,第四组
,第四组![]() ,第五组
,第五组![]() ,得到频率分布直方图如下图:
,得到频率分布直方图如下图:

(1)求实数![]() 的值;
的值;
(2)若从第二组、第五组的学生中按组用分层抽样的方法抽取9名学生组成中国海洋实地考察小队,出发前,用简单随机抽样方法从9人中抽取2人作为正、副队长,求“抽取的2人为不同组”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() 为
为![]() 边上一点,
边上一点,![]() ,
,![]() .
.

(1)证明:平面![]() 平面
平面![]() .
.
(2)若![]() ,试问:
,试问:![]() 是否与平面
是否与平面![]() 平行?若平行,求三棱锥
平行?若平行,求三棱锥![]() 的体积;若不平行,请说明理由.
的体积;若不平行,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在湖南师大附中的校园歌手大赛决赛中,有6位参赛选手(1号至6号)登台演出,由现场的100位同学投票选出最受欢迎的歌手,各位同学须彼此独立地在投票器上选出3位侯选人,其中甲同学是1号选手的同班同学,必选1号,另在2号至6号选手中随机选2名;乙同学不欣赏2号选手,必不选2号,在其他5位选手中随机选出3名;丙同学对6位选手的演唱没有偏爱,因此在1号至6号选手中随机选出3名.
(1)求同学甲选中3号且同学乙未选中3号选手的概率;
(2)设3号选手得到甲、乙、丙三位同学的票数之和为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,
,![]() 单调递增,
单调递增,![]() ,若对任意
,若对任意![]() ,存在
,存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 是
是![]() 在
在![]() 上的“追逐函数”.若
上的“追逐函数”.若![]() ,则下列四个命题:①
,则下列四个命题:①![]() 是
是![]() 在
在![]() 上的“追逐函数”;②若
上的“追逐函数”;②若![]() 是
是![]() 在
在![]() 上的“追逐函数”,则
上的“追逐函数”,则![]() ;③
;③![]() 是
是![]() 在
在![]() 上的“追逐函数”;④当
上的“追逐函数”;④当![]() 时,存在
时,存在![]() ,使得
,使得![]() 是
是![]() 在
在![]() 上的“追逐函数”.其中正确命题的个数为( )
上的“追逐函数”.其中正确命题的个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右两个焦点分别为
的左、右两个焦点分别为![]() ,P是椭圆上位于第一象限内的点,
,P是椭圆上位于第一象限内的点,![]() 轴,垂足为Q,
轴,垂足为Q,![]() ,
,![]() ,
,![]() 的面积为
的面积为![]() .
.

(1)求椭圆F的方程:
(2)若M是椭圆上的动点,求![]() 的最大值,并求出
的最大值,并求出![]() 取得最大值时M的坐标.
取得最大值时M的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,过点
,过点![]() 的直线与抛物线
的直线与抛物线![]() 相切,设第一象限的切点为
相切,设第一象限的切点为![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)若过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于两点
相交于两点![]() ,圆
,圆![]() 是以线段
是以线段![]() 为直径的圆过点
为直径的圆过点![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0),四点P1(1,1),P2(0,1),P3(–1,
(a>b>0),四点P1(1,1),P2(0,1),P3(–1, ![]() ),P4(1,
),P4(1, ![]() )中恰有三点在椭圆C上.
)中恰有三点在椭圆C上.
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为–1,证明:l过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了了解民众对开展创建文明城市工作以来的满意度,随机调查了40名群众,并将他们随机分成![]() ,
,![]() 两组,每组20人,
两组,每组20人,![]() 组群众给第一阶段的创文工作评分,
组群众给第一阶段的创文工作评分,![]() 组群众给第二阶段的创文工作评分,根据两组群众的评分绘制了如图所示的茎叶图.
组群众给第二阶段的创文工作评分,根据两组群众的评分绘制了如图所示的茎叶图.
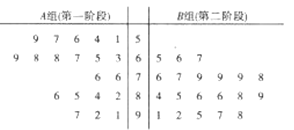
(Ⅰ)根据茎叶图比较群众对两个阶段的创文工作满意度评分的平均值和集中程度(不要求计算出具体值,给出结论即可);
(Ⅱ)完成下面的列联表,并通过计算判断是否有![]() 的把握认为民众对两个阶段创文工作的满意度存在差异?
的把握认为民众对两个阶段创文工作的满意度存在差异?
低于70分 | 不低于70分 | 合计 | |
第一阶段 | |||
第二阶段 | |||
合计 |
参考公式:![]() ,
,![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com