
【题目】已知集合![]() ,对于集合
,对于集合![]() 的两个非空子集
的两个非空子集![]() ,
, ![]() ,若
,若![]() ,则称
,则称![]() 为集合
为集合![]() 的一组“互斥子集”.记集合
的一组“互斥子集”.记集合![]() 的所有“互斥子集”的组数为
的所有“互斥子集”的组数为![]() (视
(视![]() 与
与![]() 为同一组“互斥子集”).
为同一组“互斥子集”).
(1)写出![]() ,
, ![]() ,
, ![]() 的值;
的值;
(2)求![]() .
.
 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:
【题目】已知点A(﹣ ![]() ,0),B(
,0),B( ![]() ,0),动点E满足直线EA与直线EB的斜率之积为﹣
,0),动点E满足直线EA与直线EB的斜率之积为﹣ ![]() .
.
(1)求动点E的轨迹C的方程;
(2)设过点F(1,0)的直线l1与曲线C交于点P,Q,记点P到直线l2:x=2的距离为d. 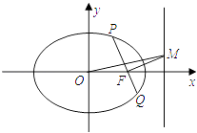
(ⅰ)求 ![]() 的值;
的值;
(ⅱ)过点F作直线l1的垂线交直线l2于点M,求证:直线OM平分线段PQ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四边形ABCD是边长为1的正方形,PA⊥平面ABCD,N是PC的中点.
(Ⅰ)若PA=1,求二面角B﹣PC﹣D的大小;
(Ⅱ)求AN与平面PCD所成角的正弦值的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如下.则下面结论中错误的一个是( ) 
A.甲的极差是29
B.乙的众数是21
C.甲罚球命中率比乙高
D.甲的中位数是24
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}中,a1=2,a4=16.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若a3 , a5分别为等差数列{bn}的第4项和第16项,试求数列{bn}的前项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人进行两种游戏,两种游戏规则如下:游戏Ⅰ:口袋中有质地、大小完全相同的5个球,编号分别为1,2,3,4,5,甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.游戏Ⅱ:口袋中有质地、大小完全相同的6个球,其中4个白球,2个红球,由裁判有放回的摸两次球,即第一次摸出记下颜色后放回再摸第二次,摸出两球同色算甲赢,摸出两球不同色算乙赢.
(Ⅰ)求游戏Ⅰ中甲赢的概率;
(Ⅱ)求游戏Ⅱ中乙赢的概率;并比较这两种游戏哪种游戏更公平?试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com