
| y 作品数量 x |
实用性 | |||||
| 1分 | 2分 | 3分 | 4分 | 5分 | ||
创 新 性 |
1分 | 1 | 3 | 1 | 0 | 1 |
| 2分 | 1 | 0 | 7 | 5 | 1 | |
| 3分 | 2 | 1 | 0 | 9 | 3 | |
| 4分 | 1 | b | 6 | 0 | a | |
| 5分 | 0 | 0 | 1 | 1 | 3 | |
| 167 |
| 50 |
| 6 |
| 50 |
| y | 1 | 2 | 3 | 4 | 5 | ||||||||||
| P |
|
|
|
|
|
| 167 |
| 50 |
| 5 |
| 50 |
| b+4 |
| 50 |
| 15 |
| 50 |
| 15 |
| 50 |
| a+8 |
| 50 |
| 167 |
| 50 |


科目:高中数学 来源:2011届湖南省长沙市长望浏宁四县高三3月调研考试数学理卷 题型:解答题
(本 小题满分12分)
小题满分12分)
某地区举办科技创新大赛,有50件科技作品参赛,大赛组委会对这50件作品分别
从“创新性”和“实用性”两项进行评分,每项评分均按等级采用5分制,若设“创新性”得分为 ,“实用性”得分为
,“实用性”得分为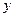 ,统计结果如下表:
,统计结果如下表:
 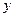 作品数量  | 实用性 | |||||
| 1分 | 2分 | 3分 | 4分 | 5分 | ||
| 创 新 性 | 1分 | 1 | 3 | 1 | 0 | 1 |
| 2分 | 1 | 0 | 7 | 5 | 1 | |
| 3分 | 2 | 1 | 0 | 9 | 3 | |
| 4分 | 1 |  | 6 | 0 | 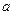 | |
| 5分 | 0 | 0 | 1 | 1 | 3 | |
 ,求
,求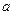 、
、 的值.
的值.查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省长沙市长望浏宁四县高三3月调研考试数学理卷 题型:解答题
(本小题满分12分)
某地区举办科技创新大赛,有50件科技作品参赛,大赛组委会对这50件作品分别
从“创新性”和“实用性”两项进行评分,每项评分均按等级采用5分制,若设“创新性”得分为 ,“实用性”得分为
,“实用性”得分为 ,统计结果如下表:
,统计结果如下表:
|
作品数量
|
实用性 |
|||||
|
1分 |
2分 |
3分 |
4分 |
5分 |
||
|
创 新 性 |
1分 |
1 |
3 |
1 |
0 |
1 |
|
2分 |
1 |
0 |
7 |
5 |
1 |
|
|
3分 |
2 |
1 |
0 |
9 |
3 |
|
|
4分 |
1 |
|
6 |
0 |
|
|
|
5分 |
0 |
0 |
1 |
1 |
3 |
(1)求“创新性为4分且实用性为3分”的概率;
(2)若“实用性”得分的数学期望为 ,求
,求 、
、 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市石景山区高三(上)期末数学试卷(理科)(解析版) 题型:解答题
| y 作品数量 x | 实用性 | |||||
| 1分 | 2分 | 3分 | 4分 | 5分 | ||
创 新 性 | 1分 | 1 | 3 | 1 | 1 | |
| 2分 | 1 | 7 | 5 | 1 | ||
| 3分 | 2 | 1 | 9 | 3 | ||
| 4分 | 1 | b | 6 | a | ||
| 5分 | 1 | 1 | 3 | |||
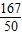 ,求a、b的值.
,求a、b的值.查看答案和解析>>
科目:高中数学 来源:2011年安徽省阜阳市太和县第二职业高级中学高三质量检测数学试卷4(理科)(解析版) 题型:解答题
| y 作品数量 x | 实用性 | |||||
| 1分 | 2分 | 3分 | 4分 | 5分 | ||
创 新 性 | 1分 | 1 | 3 | 1 | 1 | |
| 2分 | 1 | 7 | 5 | 1 | ||
| 3分 | 2 | 1 | 9 | 3 | ||
| 4分 | 1 | b | 6 | a | ||
| 5分 | 1 | 1 | 3 | |||
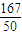 ,求a、b的值.
,求a、b的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com