
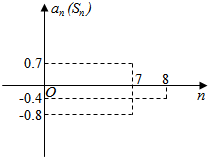 已知等差数列{an}的前n项和为Sn,在同一坐标系中,an=f(n)及Sn=g(n)的部分图象如图所示.
已知等差数列{an}的前n项和为Sn,在同一坐标系中,an=f(n)及Sn=g(n)的部分图象如图所示.分析 (1)由图象可知可能有①a7=0.7,S7=-0.8,a8=-0.4、②a7=0.7,S7=-0.8,S8=-0.4、③a7=-0.8,S7=0.7,a8=-0.4、④a7=-0.8,S7=0.7,S8=-0.4四种情况,分别利用等差数列的通项公式及其前n项和公式计算即得结论;
(2)通过(1)可知an=1.3-0.3n,从而bn=$\frac{1.3-0.3n}{{2}^{n}}$,利用错位相减法计算可知Tn=$\frac{7}{10}$-$\frac{7-3n}{10}$•$\frac{1}{{2}^{n}}$,通过$\frac{7-3n}{10}$•$\frac{1}{{2}^{n}}$在n=4时取最小值,计算即得结论.
解答 (1)解:由图象可知可能:①a7=0.7,S7=-0.8,a8=-0.4,
由a7=0.7,a8=-0.4,可得d=-1.1,a1=7.3,
∴S7=$\frac{7×(7.3+0.7)}{2}$>0,与S7=-0.8,矛盾,舍去;
②a7=0.7,S7=-0.8,S8=-0.4,
由S7=-0.8,S8=-0.4,可得a8=0.4,
∴$\frac{8×({a}_{1}+0.4)}{2}$=-0.4,解得a1=-0.5,
∴a8=-0.5+7d,解得d=$\frac{9}{70}$≠0.4-0.7=-0.3,矛盾,舍去;
③a7=-0.8,S7=0.7,a8=-0.4,
由a7=-0.8,S7=0.7,可得$\frac{7×({a}_{1}-0.8)}{2}$=0.7,解得a1=1,
∴-0.8=1+6d,解得d=-0.3,
而-0.4-(-0.8)=0.4,矛盾,舍去;
④a7=-0.8,S7=0.7,S8=-0.4,
由a7=-0.8,S7=0.7,可得$\frac{7×({a}_{1}-0.8)}{2}$=0.7,解得a1=1,
∴-0.8=1+6d,解得d=-0.3,
∴a8=-0.8-0.3=-1.1,
∴S8=0.7-1.1=-0.4,满足条件;
综上所述,a1=1、d=-0.3,
∴an=1-0.3(n-1)=1.3-0.3n;
(2)证明:由(1)可知an=1.3-0.3n,
∴bn=$\frac{{a}_{n}}{{2}^{n}}$=$\frac{1.3-0.3n}{{2}^{n}}$,
∴Tn=b1+b2+…+bn=1×$\frac{1}{2}$+0.7×$\frac{1}{{2}^{2}}$+…+(1.3-0.3n)×$\frac{1}{{2}^{n}}$,
$\frac{1}{2}$Tn=1×$\frac{1}{{2}^{2}}$+0.7×$\frac{1}{{2}^{3}}$+…+(1.6-0.3n)×$\frac{1}{{2}^{n}}$+(1.3-0.3n)×$\frac{1}{{2}^{n+1}}$,
错位相减得:$\frac{1}{2}$Tn=$\frac{1}{2}$-0.3($\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n}}$)-(1.3-0.3n)×$\frac{1}{{2}^{n+1}}$
=$\frac{1}{2}-\frac{3}{10}$•$\frac{\frac{1}{4}(1-\frac{1}{{2}^{n-1}})}{1-\frac{1}{2}}$-(1.3-0.3n)×$\frac{1}{{2}^{n+1}}$
=$\frac{1}{2}$-$\frac{3}{20}$+$\frac{3}{10}$•$\frac{1}{{2}^{n}}$-$\frac{13-3n}{20}$•$\frac{1}{{2}^{n}}$
=$\frac{7}{20}$-$\frac{7-3n}{20}$•$\frac{1}{{2}^{n}}$,
∴Tn=$\frac{7}{10}$-$\frac{7-3n}{10}$•$\frac{1}{{2}^{n}}$,
∵$\frac{7-3n}{10}$•$\frac{1}{{2}^{n}}$在n=4时取最小值,
∴Tn≤T4=$\frac{7}{10}$-$\frac{7-3×4}{10}$•$\frac{1}{{2}^{4}}$
=$\frac{7}{10}$-$\frac{-5}{160}$
=$\frac{117}{160}$.
点评 本题考查了等差数列的通项公式及其前n项和公式,考查了错位相减法,考查了数形结合的思想方法、分类讨论的方法,考查了推理能力与计算能力,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $(\frac{a}{4},0)$ x=-$\frac{a}{4}$ | B. | $(0,\frac{a}{4})$ y=-$\frac{a}{4}$ | C. | $(\frac{1}{4a},0)$ x=-$\frac{1}{4a}$ | D. | $(0,\frac{1}{4a})$ y=-$\frac{1}{4a}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>$\sqrt{2}$ | B. | a>$\sqrt{2}$或a<-$\sqrt{2}$ | C. | a<-$\sqrt{2}$ | D. | a<-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com