
【题目】在四棱锥![]() 中,
中,![]() 平面ABCD,底面四边形ABCD为等腰梯形,且
平面ABCD,底面四边形ABCD为等腰梯形,且![]() ,E,F分别为AB,PD的中点.
,E,F分别为AB,PD的中点.
(1)求证:![]() ;
;
(2)求点C到平面DEF的距离.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为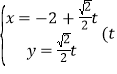 为参数
为参数![]() ,直线
,直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)若点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值;
的值;
(2)求曲线![]() 的内接矩形周长的最大值.
的内接矩形周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,(其中
,(其中![]() ,
, ![]() 为自然对数的底数,
为自然对数的底数, ![]() ……).
……).
(1)令![]() ,若
,若![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的值;
的值;
(2)在(1)的条件下,设![]() 为整数,且对于任意正整数
为整数,且对于任意正整数![]() ,
, ![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】广东省的生产总值已经连续30年位居全国第一位,如表是广东省从2012年至2018年7年的生产总值以人民币(单位:万亿元)计算的数据:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
广东省生产总值y(单位:万亿元) | 5.71 | 6.25 | 6.78 | 7.28 | 8.09 | 8.97 | 9.73 |
(1)从表中数据可认为x和y的线性相关性较强,求出以x为解释变量、y为预报变量的线性回归方程(系数精确到0.01);
(2)广东省2018年人口约为1.13亿,德国2018年人口约为0.83亿.从人口数量比较看,广东省比德国人口多,但德国2018年的生产总值为4.00万亿美元,以(1)的结论为依据,预测广东省在哪年的生产总值能超过德国在2018年的生产总值?
参考数据:![]() yi=52.81,
yi=52.81,![]() xiyi=230.05,
xiyi=230.05,![]() yi2=411.2153,
yi2=411.2153,![]() xi2=140.
xi2=140.
货币兑换:1美元≈7.03元人民币
参考公式:回归方程![]() x
x![]() 中斜率
中斜率![]() 和截距
和截距![]() 的最小二乘估计公式分别为:
的最小二乘估计公式分别为: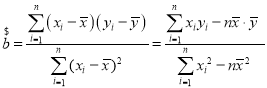 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为![]() (
(![]() 为参数).以坐标原点O为极,z轴正半轴为极轴建立极坐标系,直线
为参数).以坐标原点O为极,z轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线C的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点![]() .若直线
.若直线![]() 与曲线C相交于A,B两点,求
与曲线C相交于A,B两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数组![]() ,如果数组
,如果数组![]() 满足
满足![]() ,且
,且![]() ,其中
,其中![]()
![]() ,则称
,则称![]() 为
为![]() 的“兄弟数组”.
的“兄弟数组”.
(1)写出数组![]() 的“兄弟数组”
的“兄弟数组”![]() ;
;
(2)若![]() 的“兄弟数组”是
的“兄弟数组”是![]() ,试证明:
,试证明:![]() 成等差数列;
成等差数列;
(3)若![]() 为偶数,且
为偶数,且![]() 的“兄弟数组”是
的“兄弟数组”是![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com