
【题目】在五面体![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() .
.

(1)证明:直线![]() 平面
平面![]() ;
;
(2)已知![]() 为棱
为棱![]() 上的点,试确定
上的点,试确定![]() 点位置,使二面角
点位置,使二面角![]() 的大小为
的大小为![]() .
.
【答案】(1)证明见解析;(2)![]() 点在靠近
点在靠近![]() 点的
点的![]() 的三等分点处.
的三等分点处.
【解析】试题分析:(1)证明一条直线垂直一个平面,只需要证明这两个平面垂直,直线垂直两个平面的交线即可,先证明![]() ,
, ![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,即可得到直线
,即可得到直线![]() 平面
平面![]() ;(2)根据题意,取
;(2)根据题意,取![]() 的中点
的中点![]() ,证明
,证明![]() 两两垂直,以
两两垂直,以![]() 为原点,
为原点, ![]() 的方向为
的方向为![]() 轴,建立空间直角坐标系,由二面角
轴,建立空间直角坐标系,由二面角![]() 的大小为
的大小为![]() ,根据空间向量夹角余弦公式列方程即可确定
,根据空间向量夹角余弦公式列方程即可确定![]() 在棱
在棱![]() 上的位置.
上的位置.
试题解析:(1)![]() 四边形
四边形![]() 为菱形,
为菱形, ![]() ,
, ![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() 平面
平面![]() ,又
,又![]() 直线
直线![]() 平面
平面![]() .
.

(2) ![]() ,
, ![]() 为正三角形,取
为正三角形,取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,
, ![]() 平面
平面![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() 平面
平面![]() 两两垂直,以
两两垂直,以![]() 为原点,
为原点, ![]() 的方向为
的方向为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系, ![]() ,
, ![]() ,由(1)知
,由(1)知![]() 是平面
是平面![]() 的法向量,
的法向量, ![]() ,设
,设![]() ,则
,则![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,
, 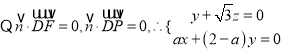 ,令
,令![]() ,则
,则![]() ,
, ![]() ,
, ![]() 二面角
二面角![]() 为
为![]() ,
, 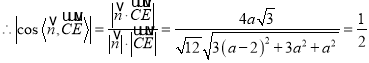 ,解得
,解得![]() ,
, ![]() 在靠近
在靠近![]() 点的三等分处.
点的三等分处.
【方法点晴】本题主要考查线面垂直的判定定理以及用空间向量求二面角,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.


 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线C:4x2﹣y2=4及直线l:y=kx﹣1
(1)求双曲线C的渐近线方程及离心率;
(2)直线l与双曲线C左右两支各有一个公共点,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn=2an﹣2,数列{bn}满足b1=1,且bn+1=bn+2.
(1)求数列{an},{bn}的通项公式;
(2)设cn= ![]() ,求数列{cn}的前2n项和T2n .
,求数列{cn}的前2n项和T2n .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log ![]()
![]() 的图象关于原点对称,其中a为常数.
的图象关于原点对称,其中a为常数.
(1)求a的值;
(2)当x∈(1,+∞)时,f(x)+log ![]() (x+1)<m恒成立,求实数m的取值范围;
(x+1)<m恒成立,求实数m的取值范围;
(3)若关于x的方程f(x)=log ![]() (x+k)在[2,3]上有解,求k的取值范围.
(x+k)在[2,3]上有解,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年3月29日,中国自主研制系全球最大水陆两栖飞机AG600将于2017年5月计划首飞,AG600飞机的用途很多,最主要的是森林灭火、水上救援、物资运输、海洋探测、根据灾情监测情报部门监测得知某个时间段全国有10起灾情,其中森林灭火2起,水上救援3起,物资运输5起,现从10起灾情中任意选取3起.
(1)求三种类型灾情中各取到1个的概率;
(2)设![]() 表示取到的森林灭火的数目,求
表示取到的森林灭火的数目,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的通项公式为an=25﹣n , 数列{bn}的通项公式为bn=n+k,设cn= ![]() 若在数列{cn}中,c5≤cn对任意n∈N*恒成立,则实数k的取值范围是 .
若在数列{cn}中,c5≤cn对任意n∈N*恒成立,则实数k的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二(4)班有男生28人,女生21人,用分层抽样的方法从全班学生中抽取一个调查小组,调查该校学生对2013年1月1日起执行的新交规的知晓情况,已知某男生被抽中的概率为 ![]() ,则抽取的女生人数为 .
,则抽取的女生人数为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的定义域为
的定义域为![]() (
(![]() ).
).
(1)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(2)若函数![]() 在定义域上是减函数,求
在定义域上是减函数,求![]() 的取值范围;
的取值范围;
(3)求函数![]() 在定义域上的最大值及最小值,并求出函数取最值时
在定义域上的最大值及最小值,并求出函数取最值时![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com