练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    有以下四个命题：
    ①函数y=sin2x和图象可以由y=sin(2x+
    π
    4
    )    向右平移
    π
    4
    个单位而得到；
    ②在△ABC中，若bcosB=ccosC，则△ABC一定是等腰三角形；
    ③|x|＞3是x＞4的必要条件；
    ④已知函数f（x）=sinx+lnx，则f′（1）的值为1+cos1．写出所有真命题的序号 ______．
    ①y=sin(2x+
    π
    4
    )    向右平移
    π
    4
    得到y=sin(2(x-
    π
    4
    )+
    π
    4
    )=sin(2x-
    π
    4
    )    ，故①错误；
    ②由bcosB=ccosC结合正弦定理可得sinBcosB=sinCcosC，即sin2B=sin2C，所以B=C或B+C=
    π
    2
    ，故②错误，
    也可用余弦定理统一成边找关系；
    ③|x|＞3?x＞3或x＜-3，故x＞4?|x|＞3，反之不成立，命题正确；
    ④f′(x)=cosx+
    1
    x
    ，故f′（1）的值为1+cos1正确，
    故答案为：③④
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    有以下四个命题：
    ①函数y=sin2x和图象可以由y=sin(2x+
    π
    4
    )    向右平移
    π
    4
    个单位而得到；
    ②在△ABC中，若bcosB=ccosC，则△ABC一定是等腰三角形；
    ③|x|＞3是x＞4的必要条件；
    ④已知函数f（x）=sinx+lnx，则f′（1）的值为1+cos1．写出所有真命题的序号
     
    ．

    查看答案和解析>>

    科目：高中数学 来源：山东省莘县实验高中2010届高三上学期模拟考试数学理科试题 题型：022

    有以下四个命题：

    ①函数y＝sin2x的图像可以由y＝sin(2x＋)向右平移个单位而得到；

    ②在△ABC中，若bcosB＝ccosC，则△ABC一定是等腰三角形；

    ③函数y＝log2x＋x2－2在(1，2)内只有一个零点；

    ④|x|＞3是x＞4的必要条件．

    其中真命题的序号是________(写出所有真命题的序号)．

    查看答案和解析>>

    科目：高中数学 来源：2009-2010学年山东省济宁一中高三（上）第一次反馈练习数学试卷（文科）（解析版） 题型：填空题

    有以下四个命题：
    ①函数y=sin2x和图象可以由向右平移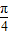个单位而得到；
    ②在△ABC中，若bcosB=ccosC，则△ABC一定是等腰三角形；
    ③|x|＞3是x＞4的必要条件；
    ④已知函数f（x）=sinx+lnx，则f′（1）的值为1+cos1．写出所有真命题的序号     ．

    查看答案和解析>>

    科目：高中数学 来源：2010年山东省济宁一中高考数学一模试卷（文科）（解析版） 题型：填空题

    有以下四个命题：
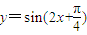    ①函数y=sin2x和图象可以由向右平移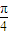个单位而得到；
    ②在△ABC中，若bcosB=ccosC，则△ABC一定是等腰三角形；
    ③|x|＞3是x＞4的必要条件；
    ④已知函数f（x）=sinx+lnx，则f′（1）的值为1+cos1．写出所有真命题的序号     ．

    查看答案和解析>>

    同步练习册答案