
【题目】如图,已知三棱锥O-ABC的三条侧棱OA,OB,OC两两垂直, ![]() 为等边三角形,
为等边三角形, ![]() 为
为![]() 内部一点,点
内部一点,点![]() 在
在![]() 的延长线上,且PA=PB.
的延长线上,且PA=PB.
(Ⅰ)证明:OA=OB;
(Ⅱ)证明:平面PAB平面POC.

科目:高中数学 来源: 题型:
【题目】近年电子商务蓬勃发展, ![]() 年某网购平台“双
年某网购平台“双![]() ”一天的销售业绩高达
”一天的销售业绩高达![]() 亿元人民币,平台对每次成功交易都有针对商品和快递是否满意的评价系统.从该评价系统中选出
亿元人民币,平台对每次成功交易都有针对商品和快递是否满意的评价系统.从该评价系统中选出![]() 次成功交易,并对其评价进行统计,网购者对商品的满意率为
次成功交易,并对其评价进行统计,网购者对商品的满意率为![]() ,对快递的满意率为
,对快递的满意率为![]() ,其中对商品和快递都满意的交易为
,其中对商品和快递都满意的交易为![]() 次.
次.
(1)根据已知条件完成下面的![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“网购者对商品满意与对快递满意之间有关系”?
的把握认为“网购者对商品满意与对快递满意之间有关系”?
对快递满意 | 对快递不满意 | 合计 | |
对商品满意 |
| ||
对商品不满意 | |||
合计 |
|
(2)为进一步提高购物者的满意度,平台按分层抽样方法从中抽取![]() 次交易进行问卷调查,详细了解满意与否的具体原因,并在这
次交易进行问卷调查,详细了解满意与否的具体原因,并在这![]() 次交易中再随机抽取
次交易中再随机抽取![]() 次进行电话回访,听取购物者意见.求电话回访的
次进行电话回访,听取购物者意见.求电话回访的![]() 次交易至少有一次对商品和快递都满意的概率.
次交易至少有一次对商品和快递都满意的概率.
附: 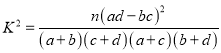 (其中
(其中![]() 为样本容量)
为样本容量)
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 是中心在原点,焦点在
是中心在原点,焦点在![]() 轴上的双曲线的右支,它的离心率刚好是其对应双曲线的实轴长,且一条渐近线方程是
轴上的双曲线的右支,它的离心率刚好是其对应双曲线的实轴长,且一条渐近线方程是![]() ,线段
,线段![]() 是过曲线
是过曲线![]() 右焦点
右焦点![]() 的一条弦,
的一条弦,![]() 是弦
是弦![]() 的中点。
的中点。
(1)求曲线![]() 的方程;
的方程;
(2)求点![]() 到
到![]() 轴距离的最小值;
轴距离的最小值;
(3)若作出直线![]() ,
,![]() 使点
使点![]() 在直线
在直线![]() 上的射影
上的射影![]() 满足
满足![]() .当点
.当点![]() 在曲线
在曲线![]() 上运动时,求
上运动时,求![]() 的取值范围.
的取值范围.
(参考公式:若![]() 为双曲线
为双曲线![]() 右支上的点,
右支上的点,![]() 为右焦点,则
为右焦点,则![]() .(
.(![]() 为离心率))
为离心率))
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln x+ax2-2x,(a∈R,a≠0)
(1)若函数f(x)的图象在x=1处的切线与x轴平行,求f(x)的单调区间;
(2)若f(x)≤ax在x∈[![]() ,+∞)上恒成立,求a的取值范围.
,+∞)上恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,点
,点![]() 与抛物线
与抛物线![]() 的焦点
的焦点![]() 关于原点对称,过点
关于原点对称,过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于不同两点
交于不同两点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于两点
交于两点![]() .
.
(Ⅰ)判断是否存在实数![]() 使得四边形
使得四边形![]() 为平行四边形.若存在,求出
为平行四边形.若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(Ⅱ)求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P—ABCD的底面是边长为a的棱形,PD⊥底面ABCD.

(1)证明:AC⊥平面PBD;
(2)若PD=AD,直线PB与平面ABCD所成的角为45°,四棱锥P—ABCD的体积为![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 中,
中,![]() 在直线
在直线![]() .
.
(1)求数列{an}的通项公式;
(2)令![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() .
.
(ⅰ)求![]() ;
;
(ⅱ)是否存在整数λ![]() ,使得不等式(-1)nλ<
,使得不等式(-1)nλ<![]() (n∈N
(n∈N![]() )恒成立?若存在,求出λ的取值的集合;若不存在,请说明理由.
)恒成立?若存在,求出λ的取值的集合;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对应的边分别为a,b,c,已知b=1,c=2且2cosA(bcosC+ccosB)=a,则A=__________;若M为边BC的中点,则|AM|=__________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com