
【题目】在正三棱柱ABCA1B1C1中,已知AB=1,AA1=2,E,F,G分别是棱AA1,AC和A1C1的中点,以![]() 为正交基底,建立如图所示的空间直角坐标系F-xyz.
为正交基底,建立如图所示的空间直角坐标系F-xyz.
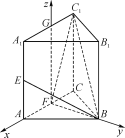
(1)求异面直线AC与BE所成角的余弦值;
(2)求二面角F-BC1-C的余弦值.
【答案】(1)![]() .(2)
.(2)![]() .
.
【解析】
(1)先根据空间直角坐标系,求得向量![]() 和向量
和向量![]() 的坐标,再利用线线角的向量方法求解.
的坐标,再利用线线角的向量方法求解.
(2)分别求得平面BFC1的一个法向量和平面BCC1的一个法向量,再利用面面角的向量方法求解.
规范解答 (1) 因为AB=1,AA1=2,则F(0,0,0),A![]() ,C
,C![]() ,B
,B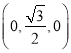 ,E
,E![]() ,
,
所以![]() =(-1,0,0),
=(-1,0,0),![]() =
=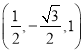
记异面直线AC和BE所成角为α,
则cosα=|cos〈![]() 〉|=
〉|=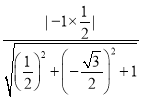 =
=![]() ,
,
所以异面直线AC和BE所成角的余弦值为![]() .
.
(2) 设平面BFC1的法向量为![]() = (x1,y1,z1).
= (x1,y1,z1).
因为![]() =
=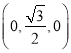 ,
,![]() =
=![]() ,
,
则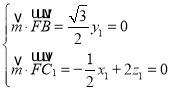
取x1=4,得平面BFC1的一个法向量为![]() =(4,0,1).
=(4,0,1).
设平面BCC1的法向量为![]() =(x2,y2,z2).
=(x2,y2,z2).
因为![]() =
=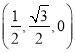 ,
,![]() =(0,0,2),
=(0,0,2),
则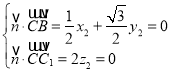
取x2=![]() 得平面BCC1的一个法向量为
得平面BCC1的一个法向量为![]() =(
=(![]() ,-1,0),
,-1,0),
所以cos〈![]() 〉=
〉= =
=![]()
根据图形可知二面角F-BC1-C为锐二面角,
所以二面角F-BC1-C的余弦值为![]() .
.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
【题目】某地有两个国家AAAA级景区—甲景区和乙景区.相关部门统计了这两个景区2019年1月至6月的客流量(单位:百人),得到如图所示的茎叶图.关于2019年1月至6月这两个景区的客流量,下列结论正确的是( )
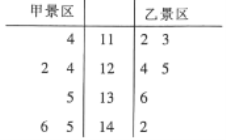
A.甲景区客流量的中位数为13000
B.乙景区客流量的中位数为13000
C.甲景区客流量的平均值比乙景区客流量的平均值小
D.甲景区客流量的极差比乙景区客流量的极差大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某艺术品公司欲生产一款迎新春工艺礼品,该礼品是由玻璃球面和该球的内接圆锥组成,圆锥的侧面用于艺术装饰,如图1.为了便于设计,可将该礼品看成是由圆![]() 及其内接等腰三角形
及其内接等腰三角形![]() 绕底边
绕底边![]() 上的高所在直线
上的高所在直线![]() 旋转180°而成,如图2.已知圆
旋转180°而成,如图2.已知圆![]() 的半径为
的半径为![]() ,设
,设![]() ,圆锥的侧面积为
,圆锥的侧面积为![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)为了达到最佳观赏效果,要求圆锥的侧面积![]() 最大.求
最大.求![]() 取得最大值时腰
取得最大值时腰![]() 的长度.
的长度.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了检验学习情况,某培训机构于近期举办一场竞赛活动,分别从甲、乙两班各抽取10名学员的成绩进行统计分析,其成绩的茎叶图如图所示(单位:分),假设成绩不低于90分者命名为“优秀学员”.
(1)分别求甲、乙两班学员成绩的平均分(结果保留一位小数);
(2)从甲班4名优秀学员中抽取两人,从乙班2名80分以下的学员中抽取一人,求三人平均分不低于90分的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,河的两岸分别有生活小区![]() 和
和![]() ,其中
,其中![]() ,
,![]() 三点共线,
三点共线,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,测得
,测得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,若以
,若以![]() 所在直线分别为
所在直线分别为![]() 轴建立平面直角坐标系
轴建立平面直角坐标系![]() 则河岸
则河岸![]() 可看成是曲线
可看成是曲线![]() (其中
(其中![]() 是常数)的一部分,河岸
是常数)的一部分,河岸![]() 可看成是直线
可看成是直线![]() (其中
(其中![]() 为常数)的一部分.
为常数)的一部分.
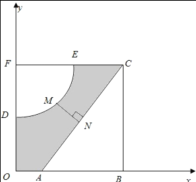
(1)求![]() 的值.
的值.
(2)现准备建一座桥![]() ,其中
,其中![]() 分别在
分别在![]() 上,且
上,且![]() ,
,![]() 的横坐标为
的横坐标为![]() .写出桥
.写出桥![]() 的长
的长![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ,并标明定义域;当
,并标明定义域;当![]() 为何值时,
为何值时,![]() 取到最小值?最小值是多少?
取到最小值?最小值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在新中国成立70周年国庆阅兵庆典中,众多群众在脸上贴着一颗红心,以此表达对祖国的热爱之情,在数学中,有多种方程都可以表示心型曲线,其中有著名的笛卡尔心型曲线,如图,在直角坐标系中,以原点O为极点,x轴正半轴为极轴建立极坐标系.图中的曲线就是笛卡尔心型曲线,其极坐标方程为![]() (
(![]() ),M为该曲线上的任意一点.
),M为该曲线上的任意一点.
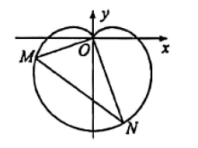
(1)当![]() 时,求M点的极坐标;
时,求M点的极坐标;
(2)将射线OM绕原点O逆时针旋转![]() 与该曲线相交于点N,求
与该曲线相交于点N,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com