
【题目】在几何体![]() 中,如图,四边形
中,如图,四边形![]() 为平行四边形,
为平行四边形,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)由![]() ,得到平面
,得到平面![]() ,平面
,平面![]() ,根据平面
,根据平面![]() 平面
平面![]() ,由面面平行的性质定理得到
,由面面平行的性质定理得到![]() ,进而得到四边形
,进而得到四边形![]() 为平行四边形,再根据
为平行四边形,再根据![]() 平面
平面![]() ,得到
,得到![]() ,由
,由![]() ,得到
,得到![]() ,同理得到
,同理得到![]() ,由线面垂直的判定定理得到
,由线面垂直的判定定理得到![]() 平面
平面![]() 得证.
得证.
(2)由(1)可知,直线![]() 、
、![]() 、
、![]() 两两垂直.以
两两垂直.以![]() 为坐标原点,以
为坐标原点,以![]() 、
、![]() 、
、![]() 为坐标轴建立的空间直角坐标系
为坐标轴建立的空间直角坐标系![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,分别求得平面
,分别求得平面![]() 和平面
和平面![]() 的一个法向量
的一个法向量![]() ,代入
,代入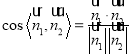 求解.
求解.
(1)证明:由![]() ,
,
可知![]() 、
、![]() 、
、![]() 、
、![]() 四点确定平面
四点确定平面![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() 四点确定平面
四点确定平面![]() .
.
∵平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
∴![]() ,四边形
,四边形![]() 为平行四边形.
为平行四边形.
同理可得,四边形![]() 为平行四边形,四边形
为平行四边形,四边形![]() 为平行四边形.
为平行四边形.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,
,
而![]() ,于是
,于是![]() .
.
由![]() ,
,![]() ,
,
则![]() .
.
由![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
∴![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,
,
∴![]() .
.
(2)由(1)可知,直线![]() 、
、![]() 、
、![]() 两两垂直.以
两两垂直.以![]() 为坐标原点,以
为坐标原点,以![]() 、
、![]() 、
、![]() 为坐标轴建立的空间直角坐标系
为坐标轴建立的空间直角坐标系![]() .
.
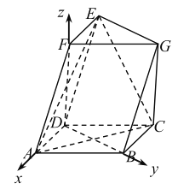
不妨设![]() ,则
,则![]() ,
,![]() .
.
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则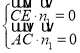 ,则
,则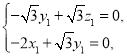 ,
,
令![]() ,则
,则![]() ,
,![]() ,
,
∴平面![]() 的一个法向量为
的一个法向量为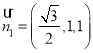 .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则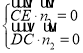 ,则
,则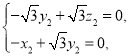 ,
,
令![]() ,则
,则![]() ,
,![]() ,
,
∴平面![]() 的一个法向量为
的一个法向量为![]() .
.
∴二面角![]() 的余弦值为
的余弦值为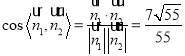 .
.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:
【题目】定义:过椭圆上的一点(不与长轴的端点重合)与椭圆的两个焦点确定的三角形称为椭圆的焦点三角形;已知过椭圆![]() 上一点P(不与长轴的端点重合)的焦点三角形
上一点P(不与长轴的端点重合)的焦点三角形![]() ,且
,且![]() .
.
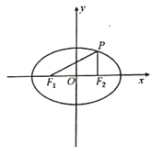
(1)求证:焦点三角形![]() 的面积为定值
的面积为定值![]() ;
;
(2)已知椭圆![]() 的一个焦点三角形为
的一个焦点三角形为![]() ,
,![]() ;
;
①若![]() ,求
,求![]() 点的横坐标的范围;
点的横坐标的范围;
②若![]() ,过点
,过点![]() 的直线
的直线![]() 与
与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,记
,记![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() ,F1,F2是双曲线的左右两个焦点,P在双曲线上且在第一象限,圆M是△F1PF2的内切圆.则M的横坐标为_________,若F1到圆M上点的最大距离为
,F1,F2是双曲线的左右两个焦点,P在双曲线上且在第一象限,圆M是△F1PF2的内切圆.则M的横坐标为_________,若F1到圆M上点的最大距离为![]() ,则△F1PF2的面积为___________.
,则△F1PF2的面积为___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年10月1日上午,庆祝中华人民共和国成立70周年阅兵仪式在天安门广场隆重举行,这次阅兵不仅展示了我国的科技军事力量,更是让世界感受到了中国的日新月异,去年的阅兵方阵有一个很抢眼,他们就是院校科研方阵,他们是由军事科学院,国防大学,国防科技大学联合组建,若已知甲,乙,丙三人来自上述三所学校,学位分别有学士、硕士、博士学位,现知道:①甲不是军事科学院的,②来自军事科学院的均不是博士,③乙不是军事科学院的,④乙不是博士学位,⑤来自国防科技大学的是硕士,则甲是来自哪个院校的,学位是什么( )
A.国防大学,博士B.国防科技大学,硕士
C.国防大学,学士D.军事科学院,学士
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
:![]() 的右顶点与抛物线
的右顶点与抛物线![]() :
:![]() 的焦点
的焦点![]() 重合,其离心率
重合,其离心率![]() .过
.过![]() 作两条相互垂直的直线
作两条相互垂直的直线![]() 与
与![]() ,且
,且![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,
两点,![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
如图,在四面体![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 上的动点,且
上的动点,且![]() 与
与![]() 相交于点
相交于点![]() .下列判断中:
.下列判断中:
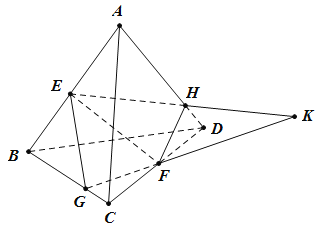
①直线![]() 经过点
经过点![]() ;
;
②![]() ;
;
③![]() 、
、![]() 、
、![]() 、
、![]() 四点共面,且该平面把四面体
四点共面,且该平面把四面体![]() 的体积分为相等的两部分.
的体积分为相等的两部分.
所有正确的序号为
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小区楼顶成一种“楔体”形状,该“楔体”两端成对称结构,其内部为钢架结构(未画出全部钢架,如图1所示,俯视图如图2所示),底面![]() 是矩形,
是矩形,![]() 米,
米,![]() 米,屋脊
米,屋脊![]() 到底面
到底面![]() 的距离即楔体的高为1.5米,钢架所在的平面
的距离即楔体的高为1.5米,钢架所在的平面![]() 与
与![]() 垂直且与底面的交线为
垂直且与底面的交线为![]() ,
,![]() 米,
米,![]() 为立柱且O是
为立柱且O是![]() 的中点.
的中点.
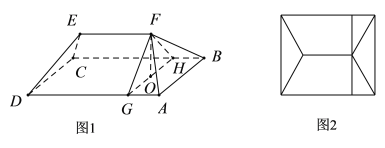
(1)求斜梁![]() 与底面
与底面![]() 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);
(2)求此模体![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com