
【题目】已知函数![]() 的定义域为
的定义域为![]() ,对于任意的
,对于任意的![]() ,都有
,都有![]() 且当
且当![]() 时,
时,![]() ,若
,若![]() .
.
(1)求证:![]() 为奇函数;
为奇函数;
(2)求证: ![]() 是
是![]() 上的减函数;
上的减函数;
(3)求函数![]() 在区间[-2,4]上的值域.
在区间[-2,4]上的值域.
【答案】(1)见解析,(2)见解析,(3) [-8,4]
【解析】
(1)先利用特殊值法,求证f(0)=0,令y=﹣x即可求证;
(2)由(1)得f(x)为奇函数,f(﹣x)=﹣f(x),利用定义法进行证明;
(3)由函数为减函数,求出f(﹣2)和f(4)继而求出函数的值域,
(1)∵f(x)的定义域为R,令x=y=0,则f(0+0)=f(0)+f(0)=2f(0),
∴f(0)=0.
令y=﹣x,则f(x﹣x)=f(x)+f(﹣x),
即f(0)=f(x)+f(﹣x)=0.
∴f(﹣x)=﹣f(x),故f(x)为奇函数.
(2)任取x1,x2∈R,且x1<x2,
则f(x2)﹣f(x1)=f(x2)+f(﹣x1)=f(x2﹣x1).
又∵x2﹣x1>0,∴f(x2﹣x1)<0,
∴f(x2)﹣f(x1)<0,
即f(x1)>f(x2).
故f(x)是R上的减函数.
(3)∵f(﹣1)=2,∴f(﹣2)=f(﹣1)+f(﹣1)=4.
又f(x)为奇函数,∴f(2)=﹣f(﹣2)=﹣4,
∴f(4)=f(2)+f(2)=﹣8.
由(2)知f(x)是R上的减函数,
所以当x=﹣2时,f(x)取得最大值,最大值为f(﹣2)=4;
当x=4时,f(x)取得最小值,最小值为f(4)=﹣8.
所以函数f(x)在区间[﹣2,4]上的值域为[﹣8,4].


科目:高中数学 来源: 题型:
【题目】甲、乙去某公司应聘面试.该公司的面试方案为:应聘者从6道备选题中一次性随机抽取3道题,按照答对题目的个数为标准进行筛选.已知6道备选题中应聘者甲有4道题能正确完成,2道题不能完成;应聘者乙每题正确完成的概率都是![]() ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(1)分别求甲、乙两人正确完成面试题数的分布列,并计算其数学期望;
(2)请分析比较甲、乙两人谁的面试通过的可能性较大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的左、右焦点为
的左、右焦点为![]() ,离心率为
,离心率为![]() ,已知过
,已知过![]() 轴上一点
轴上一点![]() 作一条直线
作一条直线![]() :
:![]() ,交椭圆于
,交椭圆于![]() 两点,且
两点,且![]() 的周长最大值为8.
的周长最大值为8.
(1)求椭圆方程;
(2)以点![]() 为圆心,半径为
为圆心,半径为![]() 的圆的方程为
的圆的方程为![]() .过
.过![]() 的中点
的中点![]() 作圆的切线
作圆的切线![]() ,
,![]() 为切点,连接
为切点,连接![]() ,证明:当
,证明:当![]() 取最大值时,点
取最大值时,点![]() 在短轴上(不包括短轴端点及原点).
在短轴上(不包括短轴端点及原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】供电部门对某社区![]() 位居民2017年12月份人均用电情况进行统计后,按人均用电量分为
位居民2017年12月份人均用电情况进行统计后,按人均用电量分为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 五组,整理得到如下的频率分布直方图,则下列说法错误的是
五组,整理得到如下的频率分布直方图,则下列说法错误的是

A. ![]() 月份人均用电量人数最多的一组有
月份人均用电量人数最多的一组有![]() 人
人
B. ![]() 月份人均用电量不低于
月份人均用电量不低于![]() 度的有
度的有![]() 人
人
C. ![]() 月份人均用电量为
月份人均用电量为![]() 度
度
D. 在这![]() 位居民中任选
位居民中任选![]() 位协助收费,选到的居民用电量在
位协助收费,选到的居民用电量在![]() 一组的概率为
一组的概率为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校研究性学习小组调查学生使用智能手机对学习成绩的影响,询问了 30 名同学,得到如下的 ![]() 列联表:
列联表:
使用智能手机 | 不使用智能手机 | 总计 | |
学习成绩优秀 | 4 | 8 | 12 |
学习成绩不优秀 | 16 | 2 | 18 |
总计 | 20 | 10 | 30 |
(Ⅰ)根据以上![]() 列联表判断,能否在犯错误的概率不超过 0.005 的前提下认为使用智能手机对学习成绩有影响?
列联表判断,能否在犯错误的概率不超过 0.005 的前提下认为使用智能手机对学习成绩有影响?
(Ⅱ)从使用学习成绩优秀的 12 名同学中,随机抽取 2 名同学,求抽到不使用智能手机的人数![]() 的分布列及数学期望.智能手机的 20 名同学中,按分层抽样的方法选出 5 名同学,求所抽取的 5 名同学中“学习成绩优秀”和“学习成绩不优秀”的人数;
的分布列及数学期望.智能手机的 20 名同学中,按分层抽样的方法选出 5 名同学,求所抽取的 5 名同学中“学习成绩优秀”和“学习成绩不优秀”的人数;
(Ⅲ)从问题(Ⅱ)中倍抽取的 5 名同学,再随机抽取 3 名同学,试求抽取 3 名同学中恰有 2 名同学为“学习成绩不优秀”的概率.
参考公式:![]() ,其中
,其中![]()
参考数据:
| 0.05 | 0,。025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构为了了解各年龄层对高考改革方案的关注程度,随机选取了200名年龄在![]() 内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分第一~五组区间分别为
内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分第一~五组区间分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
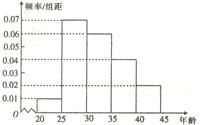
(1)求选取的市民年龄在![]() 内的人数;
内的人数;
(2)若从第3,4组用分层抽样的方法选取5名市民进行座谈,再从中选取2人在座谈会中作重点发言,求作重点发言的市民中至少有一人的年龄在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线![]() 的焦点为
的焦点为![]() ,抛物线
,抛物线![]() 上
上![]() 两点,在抛物线的准线上的射影分别为
两点,在抛物线的准线上的射影分别为![]() .
.
(1)如图,若![]() 点在线段
点在线段![]() 上,过
上,过![]() 作
作![]() 的平行线
的平行线![]() 与抛物线准线交于
与抛物线准线交于![]() ,证明:
,证明:![]() 是
是![]() 的中点;
的中点;
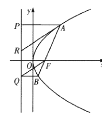
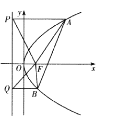
(2)如图,若![]() 的面积是
的面积是![]() 的面积的两倍,求
的面积的两倍,求![]() 中点的轨迹方程.
中点的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com