
已知等边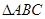 中,
中, 分别是
分别是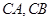 的中点,以
的中点,以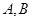 为焦点且过
为焦点且过 的椭圆和双曲线的离心率分别为
的椭圆和双曲线的离心率分别为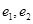 ,则下列关于
,则下列关于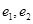 的关系式不正确的是( )
的关系式不正确的是( )
A.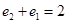 B.
B.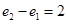 C.
C.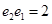 D.
D.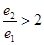
科目:高中数学 来源:2012-2013学年福建省三明市毕业班5月质量检查理科数学试卷(解析版) 题型:解答题
某企业有两个生产车间,分别位于边长是 的等边三角形
的等边三角形 的顶点
的顶点 处(如图),现要在边
处(如图),现要在边 上的
上的 点建一仓库,某工人每天用叉车将生产原料从仓库运往车间,同时将成品运回仓库.已知叉车每天要往返
点建一仓库,某工人每天用叉车将生产原料从仓库运往车间,同时将成品运回仓库.已知叉车每天要往返 车间5次,往返
车间5次,往返 车间20次,设叉车每天往返的总路程为
车间20次,设叉车每天往返的总路程为 .(注:往返一次即先从仓库到车间再由车间返回仓库)
.(注:往返一次即先从仓库到车间再由车间返回仓库)

(Ⅰ)按下列要求确定函数关系式:
①设 长为
长为 ,将
,将 表示成
表示成 的函数关系式;
的函数关系式;
②设 ,将
,将 表示成
表示成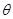 的函数关系式.
的函数关系式.
(Ⅱ)请你选用(Ⅰ)中一个合适的函数关系式,求总路程  的最小值,并指出点
的最小值,并指出点 的位置.
的位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com