练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．函数f（x）=$\frac{\sqrt{x-1}}{x-2}$的定义域为（　　）
    A．（1，+∞）B．[1，+∞）C．[1，2）D．[1，2）∪（2，+∞）

    分析 根据二次根式的性质以及分母不是0，求出函数的定义域即可．

    解答 解：由题意得：
    $\left\{\begin{array}{l}{x-1≥0}\\{x-2≠0}\end{array}\right.$，解得：x≥1且x≠2，
    故函数的定义域是[1，2）∪（2，+∞），
    故选：D．

    点评 本题考查了求函数的定义域问题，考查二次根式的性质，是一道基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    3．A={x|2-a≤x≤2+a}，B={x|（x-1）（x-4）≥0}
    （1）当a=3时，求A∩B；
    （2）若a＞0，且A∩B=∅，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．数列{an}的前n项和为Sn，a1=1，Sn=2an+1，则Sn=（　　）
    A．2n-1B．${（\frac{1}{2}）^{n-1}}$C．${（\frac{2}{3}）^{n-1}}$D．${（\frac{3}{2}）^{n-1}}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知集合A={x|x2-2x-3≥0}，集合B={x|x≥1}．
    （Ⅰ）求集合A；
    （Ⅱ）若全集U=R，求（∁UA）∪B．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点F的坐标为（1，0），且椭圆上任意一点到两焦点的距离之和为4
    （Ⅰ）求椭圆C的标准方程
    （Ⅱ）过右焦点F的直线l与椭圆C相交于P，Q两点，点Q关于x轴的对称点为Q′，试问△FPQ′的面积是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

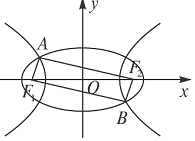    18．如图，F1，F2是椭圆${C_1}：\frac{x^2}{4}+{y^2}=1$与双曲线C2的公共焦点，A，B分别是C1，C2在第二、四象限的公共点．若四边形AF1BF2为矩形，则双曲线C2的渐近线方程是（　　）
    A．$y=±\sqrt{2}x$B．$y=±\frac{{\sqrt{2}}}{2}x$C．y=±$\sqrt{3}$xD．y=±$\frac{{\sqrt{6}}}{2}$x

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

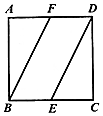    5．如图，在正方形ABCD中，点E，F分别为边BC，AD的中点，将△ABF沿BF所在直线进行翻折，将△CDE沿DE所在直线进行翻折，在翻折的过程中（　　）
    A．点A与点C在某一位置可能重合B．点A与点C的最大距离为$\sqrt{3}$AB
    C．直线AB与直线CD可能垂直D．直线AF与直线CE可能垂直

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

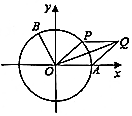    2．如图，以坐标原点O为圆心的单位圆与x轴正半轴相交于点A，点B、P在单位圆上，且B（-$\frac{\sqrt{5}}{5}$，$\frac{2\sqrt{5}}{5}$），∠AOB=α．
    （1）求$\frac{5cosα+6sinα}{4cosα-3sinα}$的值；
    （2）设∠AOP=θ（$\frac{π}{6}$≤θ≤$\frac{2π}{3}$），$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$，四边形OAQP的面积为S，f（θ）=（$\overrightarrow{OA}$•$\overrightarrow{OQ}$-$\frac{1}{2}$）2+2S2-$\frac{1}{2}$，求f（θ）的最值及此时θ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．已知θ是第四象限角，且$sin（θ+\frac{π}{4}）=\frac{3}{5}$，则cosθ=$\frac{{7\sqrt{2}}}{10}$．

    查看答案和解析>>

    同步练习册答案