
已知函数 的定义域为
的定义域为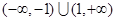 ,对定义域内的任意x,满足
,对定义域内的任意x,满足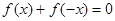 ,当
,当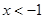 时,
时,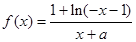 (a为常),且
(a为常),且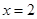 是函数
是函数 的一个极值点,
的一个极值点,
(1)求实数a的值;
(2)如果当 时,不等式
时,不等式 恒成立,求实数m的最大值;
恒成立,求实数m的最大值;
(3)求证: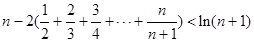
(1)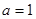 ;(2)2;(3)详见解析.
;(2)2;(3)详见解析.
解析试题分析:(1)利用 为奇函数,所以设
为奇函数,所以设 ,利用
,利用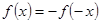 ,求出
,求出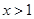 时的
时的 ,然后再求
,然后再求 时的
时的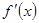 ,再根据
,再根据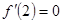 ,求出
,求出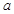 ,验证所求
,验证所求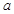 能够使
能够使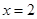 是函数
是函数 的一个极值点;(2)不等式
的一个极值点;(2)不等式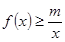 恒成立,转化为
恒成立,转化为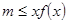 恒成立,设
恒成立,设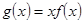 ,即求
,即求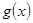 的最小值,求
的最小值,求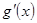
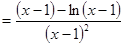 ,再设
,再设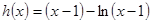 ,易求
,易求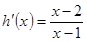 ,当
,当 时,
时,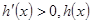 为增函数,
为增函数,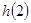 最小,
最小,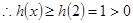 ,即
,即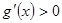 逐步分析
逐步分析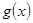 为单调递增函数,从而求得最小值.(3)通过
为单调递增函数,从而求得最小值.(3)通过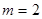 代入(2)式恒成立不等式
代入(2)式恒成立不等式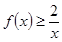 ,变形放缩后得到
,变形放缩后得到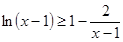 ,为出现(2)要证形式,所以令
,为出现(2)要证形式,所以令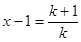 ,则
,则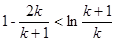 ,然后将k=1,2, n,代入上式,累加,从而得出要证不等式.此题综合性较强.
,然后将k=1,2, n,代入上式,累加,从而得出要证不等式.此题综合性较强.
试题解析:(1)由题知对定义域内任意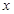 ,
,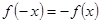 ,
,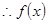 为奇函数,
为奇函数,
当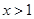 时,
时,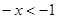 ,
, ,
,
当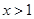 时,
时,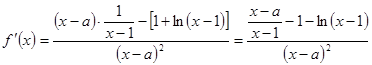
由题知: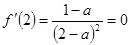 ,解得
,解得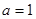 ,经验证,满足题意.
,经验证,满足题意.
(2)由(1)知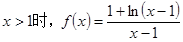
当 时,
时,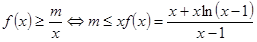 ,令
,令
则 时,
时,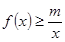 恒成立,转化为
恒成立,转化为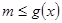 在
在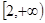 恒成立.
恒成立.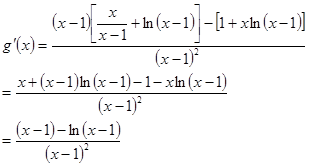
令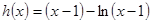 ,
,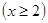 ,则
,则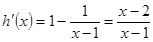 ,
,
当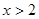 时,
时,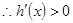 ,
,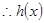 在
在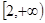 上单调递增.
上单调递增.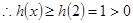
 当
当 时,
时,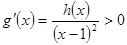 ,
,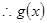 在
在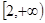 单调递增.
单调递增.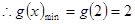
则若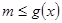 在
在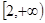 恒成立,则
恒成立,则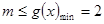
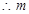 的最大值2.
的最大值2.
(3)由(2)知当 时,有
时,有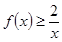 ,即
,即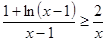
则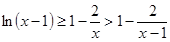
令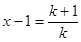 ,则
,则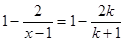


科目:高中数学 来源: 题型:解答题
为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,进行技术攻关,新上了把二氧化碳处理转化为一种可利用的化工产品的项目,经测算,该项目月处理成本y(元)与月处理量x(吨)之间的函数关系可近似地表示为
y=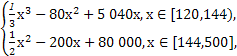
且每处理一吨二氧化碳得到可利用的化工产品价值为200元,若该项目不获利,国家将给予补偿.
(1)当x∈[200,300]时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则国家每月至少需要补贴多少元才能使该项目不亏损?
(2)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数f(x)=ax2+bx+1(a>0),F(x)=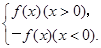 若f(-1)=0,且对任意实数x均有f(x)≥0成立.
若f(-1)=0,且对任意实数x均有f(x)≥0成立.
(1)求F(x)的表达式;
(2)当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点 的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为
的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为 米,圆心角为
米,圆心角为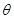 (弧度).
(弧度).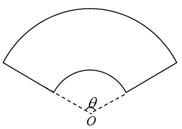
(1)求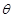 关于
关于 的函数关系式;
的函数关系式;
(2)已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为 ,求
,求 关于
关于 的函数关系式,并求出
的函数关系式,并求出 为何值时,
为何值时, 取得最大值?
取得最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某投资公司计划投资A,B两种金融产品,根据市场调查与预测,A产品的利润y1与投资金额x的函数关系为y1=18-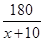 ,B产品的利润y2与投资金额x的函数关系为y2=
,B产品的利润y2与投资金额x的函数关系为y2=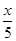 (注:利润与投资金额单位:万元).
(注:利润与投资金额单位:万元).
(1)该公司已有100万元资金,并全部投入A,B两种产品中,其中x万元资金投入A产品,试把A,B两种产品利润总和表示为x的函数,并写出定义域;
(2)在(1)的条件下,试问:怎样分配这100万元资金,才能使公司获得最大利润?其最大利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
我国加入WTO后,根据达成的协议,若干年内某产品关税与市场供应量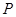 的关系允许近似的满足:
的关系允许近似的满足: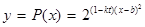 (其中
(其中 为关税的税率,且
为关税的税率,且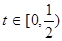 ,
, 为市场价格,
为市场价格,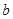 、
、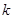 为正常数),当
为正常数),当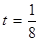 时的市场供应量曲线如图:
时的市场供应量曲线如图: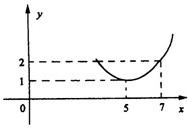
(1)根据图象求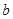 、
、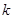 的值;
的值;
(2)若市场需求量为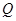 ,它近似满足
,它近似满足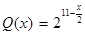 .当
.当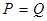 时的市场价格称为市场平衡价格.为使市场平衡价格控制在不低于9元,求税率
时的市场价格称为市场平衡价格.为使市场平衡价格控制在不低于9元,求税率 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com