为了缓解城市道路拥堵的局面,某市拟提高中心城区内占道停车场的收费标准,并实行累进加价收费.已公布的征求意见稿是这么叙述此收费标准的:“(中心城区占道停车场)收费标准为每小时10元,并实行累进加价制度,占道停放1小时后,每小时按加价50%收费.”
方案公布后,这则“累进加价”的算法却在媒体上引发了争议(可查询2010年12月14日的相关国内新闻).请你用所学的数学知识说明争议的原因,并请按照一辆普通小汽车一天内连续停车14小时测算:根据不同的解释,收费各应为多少元?
解:争议的原因是收费标准中对于“每小时按加价50%收费”的含义出现了歧义.以下给出三种不同的理解:
解释一:第一小时为10元,以后每小时都为15元.14小时总收费为:s
1=10+15×13=205元;
解释二:第一小时为10元,以后每小时都比前一小时增加5元.
可以理解为等差数列求和,则14小时总收费为s
2=14×10+
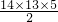
=595元.
解释三:第一小时为10元,以后每小时都增加50%.可以理解为等比数列求和,
则14个小时的收费为s
3=
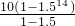
=5818.59元.
所以,理解的含义不同,所收费用也不同.
分析:争议的原因应是收费标准中对于“每小时按加价50%收费”的含义,可以有不同的理解:
解释一:第一小时为10元,以后每小时都为15元,14小时总收费为s
1元;
解释二:第一小时为10元,以后每小时都比前一小时增加5元,是等差数列求和,则14小时总收费为s
2元;
解释三:第一小时为10元,以后每小时都增加50%.为等比数列求和,则14个小时的收费为s
3元.
点评:本题考查了等差、等比数列的求和问题;通过阅读题意,建立适当的数学模型,是解答本题的关键.

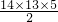 =595元.
=595元.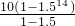 =5818.59元.
=5818.59元.
