
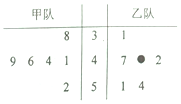
 甲乙两个竞赛队都参加了6场比赛,比赛得分情况的经营如图如图(单位:分)),其中乙队的一个得分数字被污损,那么估计乙队的平均得分大于甲队的平均得分的概率为( )
甲乙两个竞赛队都参加了6场比赛,比赛得分情况的经营如图如图(单位:分)),其中乙队的一个得分数字被污损,那么估计乙队的平均得分大于甲队的平均得分的概率为( )| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |
分析 设乙队的一个得分数字被污损的数学为x,求出甲队平均分为45.乙队平均分为$\frac{265+x}{6}$,由x的可能取值的个数是10个,满足$\frac{265+x}{6}$>45的x的个数有4个,由此能估计乙队的平均得分大于甲队的平均得分的概率.
解答 解:设乙队的一个得分数字被污损的数学为x,
甲队平均分为:$\overline{{x}_{甲}}$=$\frac{1}{6}$(38+41+44+46+49+52)=45.
乙队平均分为:$\overline{{x}_{乙}}$=$\frac{1}{6}$(31+47+40+x+42+51+54)=$\frac{265+x}{6}$,
∵x的可能取值的个数是10个,
满足$\frac{265+x}{6}$>45的x的个数有4个,
∴估计乙队的平均得分大于甲队的平均得分的概率p=$\frac{4}{10}=\frac{2}{5}$.
故选:C.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意茎叶图及等可能事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:解答题
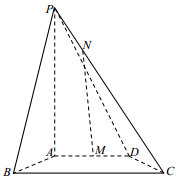 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,BC=2AD=4,AB=CD,∠ABC=60°,N为线段PC上一点,CN=3NP,M为AD的中点.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,BC=2AD=4,AB=CD,∠ABC=60°,N为线段PC上一点,CN=3NP,M为AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{3}{4}$) | B. | [$\frac{1}{2}$,$\frac{3}{4}$) | C. | ($\frac{1}{4}$,$\frac{1}{2}$) | D. | [$\frac{1}{4}$,$\frac{3}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com