
【题目】【2018广东省深中、华附、省实、广雅四校联考】已知椭圆![]() 的离心率为
的离心率为![]() ,圆
,圆![]() 与
与![]() 轴交于点
轴交于点![]() ,
, ![]() 为椭圆
为椭圆![]() 上的动点,
上的动点, ![]() ,
, ![]() 面积最大值为
面积最大值为![]() .
.
(I)求圆![]() 与椭圆
与椭圆![]() 的方程;
的方程;
(II)圆![]() 的切线
的切线![]() 交椭圆于点
交椭圆于点![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(I)圆![]() 的方程为
的方程为![]() ,椭圆
,椭圆![]() 的方程为
的方程为![]() .(II)
.(II)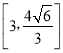
【解析】【试题分析】(1)根据离心率可有![]() ,依题意可知
,依题意可知![]() 为椭圆的焦点,故
为椭圆的焦点,故![]() .当
.当![]() 位于椭圆上顶点时,面积取得最大值,由此列方程可解得
位于椭圆上顶点时,面积取得最大值,由此列方程可解得![]() 的值,并求得圆和椭圆的方程.(2)当直线斜率存在时,设出直线方程为
的值,并求得圆和椭圆的方程.(2)当直线斜率存在时,设出直线方程为![]() ,利用圆和直线相切求得
,利用圆和直线相切求得![]() 的等量关系式,利用韦达定理和弦长公式计算出弦长并利用配方法求得弦长的取值范围.当直线斜率不存在时,直线
的等量关系式,利用韦达定理和弦长公式计算出弦长并利用配方法求得弦长的取值范围.当直线斜率不存在时,直线![]() 的方程为
的方程为![]() ,可直接得到
,可直接得到![]() 的坐标求出弦长.
的坐标求出弦长.
【试题解析】
(1)由题意得![]() ,解得:
,解得: ![]() ①
①
因为![]() ,所以,点
,所以,点![]() 为椭圆的焦点,所以,
为椭圆的焦点,所以, ![]()
设![]() ,则
,则![]() ,所以
,所以![]() ,当
,当![]() 时,
时,
![]() ,代入①解得
,代入①解得![]() ,所以
,所以![]() ,
,
所以,圆![]() 的方程为
的方程为![]() ,椭圆
,椭圆![]() 的方程为
的方程为![]() .
.
(2)①当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
, ![]()
因为直线![]() 与圆相切,所以
与圆相切,所以![]() ,即
,即![]() ,
,
联立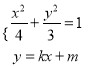 ,消去
,消去![]() 可得
可得![]() ,
,
![]() ,
,
![]()
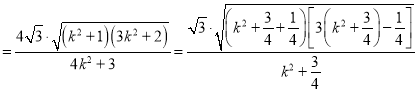
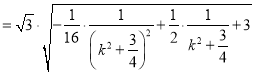
令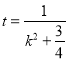 ,则
,则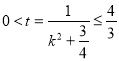 ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]()
②当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为
的方程为![]() ,解得
,解得![]() ,
,
综上, ![]() 的取值范围是
的取值范围是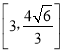 .
.


科目:高中数学 来源: 题型:
【题目】【2018天一大联考高中毕业班阶段性测试(四)】已知函数![]() ,
, ![]() .
.
(I)若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(II)证明:对于任意正整数![]() ,都有
,都有![]() 成立.
成立.
附: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
, ![]() 是等腰直角三角形
是等腰直角三角形![]() 的斜边,且
的斜边,且![]() .
.
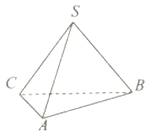
(1)求证: ![]() ;
;
(2)已知平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,且
,且![]() 到平面
到平面![]() 的距离相等,试确定直线
的距离相等,试确定直线![]() 及点
及点![]() 的位置(说明作法及理由),并求三棱锥
的位置(说明作法及理由),并求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以
为参数),在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 是圆心为
是圆心为![]() ,半径为1的圆.
,半径为1的圆.
(1)求曲线![]() ,
, ![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 为曲线
为曲线![]() 上的点,
上的点, ![]() 为曲线
为曲线![]() 上的点,求
上的点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】11月11日有2000名网购者在某购物网站进行网购消费(金额不超过1000元),其中女性1100名,男性900名.该购物网站为优化营销策略,根据性别采用分层抽样的方法从这2000名网购者中抽取200名进行分析,如表.(消费金额单位:元)

(1)计算![]() 的值,在抽出的200名且消费金额在
的值,在抽出的200名且消费金额在![]() 的网购者中随机抽出2名发放网购红包,求选出的2人均为女性的概率;
的网购者中随机抽出2名发放网购红包,求选出的2人均为女性的概率;
(2)若消费金额不低于600元的网购者为“网购达人”,低于600元的网购者为“非网购达人”,根据以上数据列![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“是否为网购达人与性别有关?”附:
的把握认为“是否为网购达人与性别有关?”附:![]() ,
,![]()

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,已知点
,已知点![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() ,动点
,动点![]() 的轨迹为
的轨迹为![]() .
.
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的极坐标为
的极坐标为![]() ,点
,点![]() 在曲线
在曲线![]() 上,求
上,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项都是正数的数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足
满足![]() ,求和
,求和![]() ;
;
(3)是否存在正整数![]() ,
,![]() ,
,![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等差数列?若存在,求出所有满足要求的
成等差数列?若存在,求出所有满足要求的![]() ,
,![]() ,
,![]() ,若不存在,说明理由.
,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com