
 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响. =
= ,
, =
= ,
,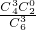 =
= ,
,| ξ | 1 | 2 | 3 |
| P |  |  |  |
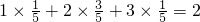 .
. ,k=0,1,2,3,
,k=0,1,2,3,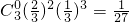 ,
, ,
, ,
,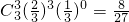 ,
,| η | 0 | 1 | 2 | 3 |
| P |  |  | 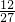 |  |
 +1×
+1× +2×
+2×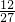 +
+ =2.
=2. +(2-2)
+(2-2)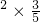 +
+ =
= ,
, +
+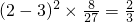 ,
, =
= ,P(ξ=2)=
,P(ξ=2)= =
= ,P(ξ=3)=
,P(ξ=3)=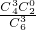 =
= ,由此能求出ξ的分布列和E(ξ).
,由此能求出ξ的分布列和E(ξ). ,D(ξ)=(2-1)2×
,D(ξ)=(2-1)2× +(2-2)
+(2-2)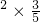 +
+ =
= ,D(η)=
,D(η)= +
+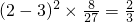 ,所以,从统计的角度可以判断考生甲这门学科的水平更好.
,所以,从统计的角度可以判断考生甲这门学科的水平更好.

 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
| 2 | 3 |
查看答案和解析>>
科目:高中数学 来源:江苏省扬州中学2011-2012学年高二下学期期中考试数学理科试卷 题型:044
某学校设计了一个实验学科的考查方案:考生从6道备选题中一次性抽取3道题,规定至少正确完成其中2道题便可通过,已知6道备选题中考生甲有4道能正确完成,2道不能完成;考生乙正确完成每道题的概率都是![]() ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(1)求甲正确完成的题数ξ的分布列及期望;求乙正确完成的题数η的分布列及期望;
(2)请用统计知识分析比较两名考生这门学科的水平.
查看答案和解析>>
科目:高中数学 来源:2013届江苏省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
某学校设计了一个实验学科的考查方案:考生从6道备选题中一次性抽取3道题,规定至少正确完成其中2道题便可通过,已知6道备选题中考生甲有4道能正确完成,2道不能完成;考生乙正确完成每道题的概率都是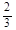 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
⑴求甲正确完成的题数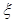 的分布列及期望;求乙正确完成的题数
的分布列及期望;求乙正确完成的题数 的分布列及期望;
的分布列及期望;
⑵请用统计知识分析比较两名考生这门学科的水平.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com