
【题目】正方形![]() 沿对角线
沿对角线![]() 折成直二面角,下列结论:①异面直线
折成直二面角,下列结论:①异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ;②
;②![]() ;③
;③![]() 是等边三角形;④二面角
是等边三角形;④二面角![]() 的平面角正切值是
的平面角正切值是![]() ;其中正确结论是______.(写出你认为正确的所有结论的序号)
;其中正确结论是______.(写出你认为正确的所有结论的序号)
科目:高中数学 来源: 题型:
【题目】已知点![]() 为椭圆
为椭圆![]() 上任意一点,直线
上任意一点,直线![]() 与圆
与圆![]() 交于
交于![]() 两点,点
两点,点![]() 为椭圆
为椭圆![]() 的左焦点.
的左焦点.
(Ⅰ)求椭圆![]() 的离心率及左焦点
的离心率及左焦点![]() 的坐标;
的坐标;
(Ⅱ)求证:直线![]() 与椭圆
与椭圆![]() 相切;
相切;
(Ⅲ)判断![]() 是否为定值,并说明理由.
是否为定值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题:
①“若![]() ,则
,则![]() ”的逆否命题为真命题
”的逆否命题为真命题
②“![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 上为增函数”的充分不必要条件
上为增函数”的充分不必要条件
③若![]() 为假命题,则
为假命题,则![]() ,
,![]() 均为假命题
均为假命题
④对于命题![]() :
:![]() ,
,![]() ,则
,则![]() 为:
为:![]() ,
,![]()
其中真命题的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果数列![]() 对于任意
对于任意![]() ,都有
,都有![]() ,其中
,其中![]() 为常数,则称数列
为常数,则称数列![]() 是“间等差数列”,
是“间等差数列”,![]() 为“间公差”.若数列
为“间公差”.若数列![]() 满足
满足![]() ,
,![]() ,
,![]() .
.
(1)求证:数列![]() 是“间等差数列”,并求间公差
是“间等差数列”,并求间公差![]() ;
;
(2)设![]() 为数列
为数列![]() 的前n项和,若
的前n项和,若![]() 的最小值为-153,求实数
的最小值为-153,求实数![]() 的取值范围;
的取值范围;
(3)类似地:非零数列![]() 对于任意
对于任意![]() ,都有
,都有![]() ,其中
,其中![]() 为常数,则称数列
为常数,则称数列![]() 是“间等比数列”,
是“间等比数列”,![]() 为“间公比”.已知数列
为“间公比”.已知数列![]() 中,满足
中,满足![]() ,
,![]() ,
,![]() ,试问数列
,试问数列![]() 是否为“间等比数列”,若是,求最大的整数
是否为“间等比数列”,若是,求最大的整数![]() 使得对于任意
使得对于任意![]() ,都有
,都有![]() ;若不是,说明理由.
;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 交
交![]() 轴于
轴于![]() 两点(
两点(![]() 不重合),交
不重合),交![]() 轴于
轴于![]() 点. 圆
点. 圆![]() 过
过![]() 三点.下列说法正确的是( )
三点.下列说法正确的是( )
① 圆心![]() 在直线
在直线![]() 上;
上;
② ![]() 的取值范围是
的取值范围是![]() ;
;
③ 圆![]() 半径的最小值为
半径的最小值为![]() ;
;
④ 存在定点![]() ,使得圆
,使得圆![]() 恒过点
恒过点![]() .
.
A. ①②③B. ①③④C. ②③D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,定义椭圆
,定义椭圆![]() 上的点
上的点![]() 的“伴随点”为
的“伴随点”为![]() .
.
(1)求椭圆![]() 上的点
上的点![]() 的“伴随点”
的“伴随点”![]() 的轨迹方程;
的轨迹方程;
(2)如果椭圆![]() 上的点
上的点![]() 的“伴随点”为
的“伴随点”为![]() ,对于椭圆
,对于椭圆![]() 上的任意点
上的任意点![]() 及它的“伴随点”
及它的“伴随点”![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)当![]() ,
, ![]() 时,直线
时,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,若点
两点,若点![]() ,
, ![]() 的“伴随点”分别是
的“伴随点”分别是![]() ,
, ![]() ,且以
,且以![]() 为直径的圆经过坐标原点
为直径的圆经过坐标原点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了组建一支业余足球队,在高一年级随机选取50名男生测量身高,发现被测男生的身高全部在![]() 到
到![]() 之间,将测量结果按如下方式分成六组:第1组
之间,将测量结果按如下方式分成六组:第1组![]() ,第2组
,第2组![]() ,…,第6组
,…,第6组![]() ,如图是按上述分组得到的频率分布直方图,以频率近似概率.
,如图是按上述分组得到的频率分布直方图,以频率近似概率.
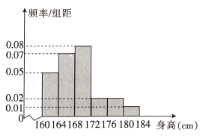
(1)若学校要从中选1名男生担任足球队长,求被选取的男生恰好在第5组或第6组的概率;
(2)试估计该校高一年级全体男生身高的平均数(同一组中的数据用该组区间的中点值代表)与中位数;
(3)现在从第5与第6组男生中选取两名同学担任守门员,求选取的两人中最多有1名男生来自第5组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com