
ЁОЬтФПЁПдВжмТЪЪЧдВЕФжмГЄгыжБОЖЕФБШжЕЃЌвЛАугУЯЃРАзжФИ![]() БэЪО.дчдкЙЋдЊ480ФъзѓгвЃЌФЯББГЏЪБЦкЕФЪ§бЇМвзцГхжЎОЭЕУГіОЋШЗЕНаЁЪ§ЕуКѓ7ЮЛЕФНсЙћЃЌЫћЪЧЪРНчЩЯЕквЛИіАбдВжмТЪЕФЪ§жЕМЦЫуЕНаЁЪ§ЕуКѓЕк7ЮЛЕФШЫЃЌетБШХЗжодчСЫдМ1000Фъ.ЩњЛюжаЃЌЮвУЧвВПЩвдЭЈЙ§ШчЯТЫцЛњФЃФтЪдбщРДЙРМЦ
БэЪО.дчдкЙЋдЊ480ФъзѓгвЃЌФЯББГЏЪБЦкЕФЪ§бЇМвзцГхжЎОЭЕУГіОЋШЗЕНаЁЪ§ЕуКѓ7ЮЛЕФНсЙћЃЌЫћЪЧЪРНчЩЯЕквЛИіАбдВжмТЪЕФЪ§жЕМЦЫуЕНаЁЪ§ЕуКѓЕк7ЮЛЕФШЫЃЌетБШХЗжодчСЫдМ1000Фъ.ЩњЛюжаЃЌЮвУЧвВПЩвдЭЈЙ§ШчЯТЫцЛњФЃФтЪдбщРДЙРМЦ![]() ЕФжЕЃКдкЧјМф
ЕФжЕЃКдкЧјМф![]() ФкЫцЛњШЁ
ФкЫцЛњШЁ![]() ИіЪ§ЃЌЙЙГЩ
ИіЪ§ЃЌЙЙГЩ![]() ИіЪ§Жд
ИіЪ§Жд![]() ЃЌЩш
ЃЌЩш![]() ЃЌ
ЃЌ![]() Фмгы1ЙЙГЩЖлНЧШ§НЧаЮШ§БпЕФЪ§Жд
Фмгы1ЙЙГЩЖлНЧШ§НЧаЮШ§БпЕФЪ§Жд![]() га
га![]() ЖдЃЌдђЭЈЙ§ЫцЛњФЃФтЕФЗНЗЈЕУЕНЕФ
ЖдЃЌдђЭЈЙ§ЫцЛњФЃФтЕФЗНЗЈЕУЕНЕФ![]() ЕФНќЫЦжЕЮЊЃЈ ЃЉ
ЕФНќЫЦжЕЮЊЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ЁОД№АИЁПC
ЁОНтЮіЁП
ИљОндкЧјМф![]() ФкЫцЛњШЁ
ФкЫцЛњШЁ![]() ИіЪ§ЃЌдђга
ИіЪ§ЃЌдђга![]() ЃЌЪдбщЕФШЋВПНсЙћЙЙГЩвд1ЮЊБпГЄЕФе§ЗНаЮЃЌЦфУцЛ§ЮЊ1.вђЮЊ
ЃЌЪдбщЕФШЋВПНсЙћЙЙГЩвд1ЮЊБпГЄЕФе§ЗНаЮЃЌЦфУцЛ§ЮЊ1.вђЮЊ![]() ЃЌ
ЃЌ![]() Фмгы1ЙЙГЩЖлНЧШ§НЧаЮЃЌгЩгрЯвЖЈРэЕФМАШ§НЧаЮжЊЪЖЕУ
Фмгы1ЙЙГЩЖлНЧШ§НЧаЮЃЌгЩгрЯвЖЈРэЕФМАШ§НЧаЮжЊЪЖЕУ ЧѓЕУЯргІЕФУцЛ§ЃЌдйРћгУМИКЮИХаЭЕФИХТЪЙЋЪНЧѓНт.
ЧѓЕУЯргІЕФУцЛ§ЃЌдйРћгУМИКЮИХаЭЕФИХТЪЙЋЪНЧѓНт.
вРЬтга![]() ЃЌЪдбщЕФШЋВПНсЙћЙЙГЩвд1ЮЊБпГЄЕФе§ЗНаЮЃЌЦфУцЛ§ЮЊ1.
ЃЌЪдбщЕФШЋВПНсЙћЙЙГЩвд1ЮЊБпГЄЕФе§ЗНаЮЃЌЦфУцЛ§ЮЊ1.
вђЮЊ![]() ЃЌ
ЃЌ![]() Фмгы1ЙЙГЩЖлНЧШ§НЧаЮЃЌ
Фмгы1ЙЙГЩЖлНЧШ§НЧаЮЃЌ
гЩгрЯвЖЈРэЕФМАШ§НЧаЮжЊЪЖЕУ ЃЌ
ЃЌ
ЙЙГЩШчЭМвѕгАВПЗжЃЌ
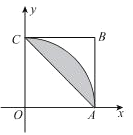
ЦфУцЛ§ЮЊ![]() ЃЌ
ЃЌ
гЩМИКЮИХаЭИХТЪМЦЫуЙЋЪНЕУ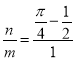 ЃЌ
ЃЌ
НтЕУ![]() .
.
ЙЪбЁЃКC



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖрУцЬх![]() ЃЌЦНУц
ЃЌЦНУц![]() ЦНУц
ЦНУц![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЪЧ
ЪЧ![]() ЩЯЕФЕу.
ЩЯЕФЕу.
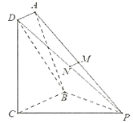
ЃЈЂёЃЉШє![]() ЦНУц
ЦНУц![]() ЃЌжЄУїЃК
ЃЌжЄУїЃК![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЛ
ЕФжаЕуЃЛ
ЃЈЂђЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓЖўУцНЧ
ЃЌЧѓЖўУцНЧ![]() ЕФЦНУцНЧЕФгрЯвжЕ.
ЕФЦНУцНЧЕФгрЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,![]() ЪЧдВзЖ
ЪЧдВзЖ![]() ЕФЕзУц
ЕФЕзУц![]() ЕФжБОЖ,
ЕФжБОЖ,![]() ЪЧдВ
ЪЧдВ![]() ЩЯвьгк
ЩЯвьгк![]() ЕФШЮвтвЛЕу,вд
ЕФШЮвтвЛЕу,вд![]() ЮЊжБОЖЕФдВгы
ЮЊжБОЖЕФдВгы![]() ЕФСэвЛИіНЛЕуЮЊ
ЕФСэвЛИіНЛЕуЮЊ![]() ЮЊ
ЮЊ![]() ЕФжаЕу.ЯжИјГівдЯТНсТлЃК
ЕФжаЕу.ЯжИјГівдЯТНсТлЃК
Ђй![]() ЮЊжБНЧШ§НЧаЮ
ЮЊжБНЧШ§НЧаЮ
ЂкЦНУц![]() ЦНУц
ЦНУц![]()
ЂлЦНУц![]() БигыдВзЖ
БигыдВзЖ![]() ЕФФГЬѕФИЯпЦНаа
ЕФФГЬѕФИЯпЦНаа
Цфжае§ШЗНсТлЕФИіЪ§ЪЧ
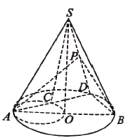
A. 0B. 1C. 2D. 3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЃЌКЏЪ§
ЃЌКЏЪ§![]() гаСНИіВЛЭЌЕФМЋжЕЕу
гаСНИіВЛЭЌЕФМЋжЕЕу![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉжЄУїЃК![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЛЊЮЊЖЪТЛсОіЖЈЭЖзЪПЊЗЂаТПюШэМўЃЌЙРМЦФмЛёЕУ![]() ЭђдЊЕН
ЭђдЊЕН![]() ЭђдЊЕФЭЖзЪЪевцЃЌЬжТлСЫвЛИіЖдПЮЬтзщЕФНБРјЗНАИ:НБН№
ЭђдЊЕФЭЖзЪЪевцЃЌЬжТлСЫвЛИіЖдПЮЬтзщЕФНБРјЗНАИ:НБН№![]() (ЕЅЮЛ:ЭђдЊ)ЫцЭЖзЪЪевц
(ЕЅЮЛ:ЭђдЊ)ЫцЭЖзЪЪевц![]() (ЕЅЮЛ:ЭђдЊ)ЕФдіМгЖјдіМгЃЌЧвНБН№ВЛГЌЙ§
(ЕЅЮЛ:ЭђдЊ)ЕФдіМгЖјдіМгЃЌЧвНБН№ВЛГЌЙ§![]() ЭђдЊЃЌЭЌЪБНБН№ВЛГЌЙ§ЭЖзЪЪевцЕФ
ЭђдЊЃЌЭЌЪБНБН№ВЛГЌЙ§ЭЖзЪЪевцЕФ![]() .
.
ЃЈ1ЃЉЧыЗжЮіКЏЪ§![]() ЪЧЗёЗћКЯЛЊЮЊвЊЧѓЕФНБРјКЏЪ§ФЃаЭЃЌВЂЫЕУїдвђЃЛ
ЪЧЗёЗћКЯЛЊЮЊвЊЧѓЕФНБРјКЏЪ§ФЃаЭЃЌВЂЫЕУїдвђЃЛ
ЃЈ2ЃЉШєЛЊЮЊЙЋЫОВЩгУФЃаЭКЏЪ§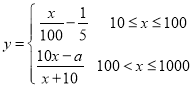 зїЮЊНБРјКЏЪ§ФЃаЭЃЌЪдШЗЖЈе§ећЪ§
зїЮЊНБРјКЏЪ§ФЃаЭЃЌЪдШЗЖЈе§ећЪ§![]() ЕФШЁжЕМЏКЯ.
ЕФШЁжЕМЏКЯ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЮФЬхОжЮЊСЫНтЁАХмЭХЁБУПдТХмВНЕФЦНОљРяГЬЃЌЪеМЏВЂећРэСЫ2018Фъ1дТжС2018Фъ11дТЦкМфЁАХмЭХЁБУПдТХмВНЕФЦНОљРяГЬЃЈЕЅЮЛЃКЙЋРяЃЉЕФЪ§ОнЃЌЛцжЦСЫЯТУцЕФелЯпЭМ.ИљОнелЯпЭМЃЌЯТСаНсТле§ШЗЕФЪЧЃЈ ЃЉ

A. дТХмВНЦНОљРяГЬЕФжаЮЛЪ§ЮЊ6дТЗнЖдгІЕФРяГЬЪ§
B. дТХмВНЦНОљРяГЬж№дТдіМг
C. дТХмВНЦНОљРяГЬИпЗхЦкДѓжТдк8ЁЂ9дТ
D. 1дТжС5дТЕФдТХмВНЦНОљРяГЬЯрЖдгк6дТжС11дТЃЌВЈЖЏадИќаЁЃЌБфЛЏБШНЯЦНЮШ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжааФдкдЕуЕФЭждВEЕФвЛИіНЙЕугыХзЮяЯп![]() ЕФНЙЕуЙигкжБЯп
ЕФНЙЕуЙигкжБЯп![]() ЖдГЦЃЌЧвЭждВEгызјБъжсЕФвЛИіНЛЕузјБъЮЊ
ЖдГЦЃЌЧвЭждВEгызјБъжсЕФвЛИіНЛЕузјБъЮЊ![]() .
.
ЃЈ1ЃЉЧѓЭждВEЕФБъзМЗНГЬЃЛ
ЃЈ2ЃЉЙ§Еу![]() ЕФжБЯпlЃЈжБЯпЕФаБТЪkДцдкЧвВЛЮЊ0ЃЉНЛEгкAЃЌBСНЕуЃЌНЛxжсгкЕуPЕуAЙигкxжсЕФЖдГЦЕуЮЊDЃЌжБЯпBDНЛxжсгкЕуQ.ЪдЬНОП
ЕФжБЯпlЃЈжБЯпЕФаБТЪkДцдкЧвВЛЮЊ0ЃЉНЛEгкAЃЌBСНЕуЃЌНЛxжсгкЕуPЕуAЙигкxжсЕФЖдГЦЕуЮЊDЃЌжБЯпBDНЛxжсгкЕуQ.ЪдЬНОП![]() ЪЧЗёЮЊЖЈжЕЃПЧыЫЕУїРэгЩ.
ЪЧЗёЮЊЖЈжЕЃПЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЈ1ЃЉЃЌдкЕШбќжБНЧ![]() жаЃЌаББп
жаЃЌаББп![]() ЃЌDЮЊ
ЃЌDЮЊ![]() ЕФжаЕуЃЌНЋ
ЕФжаЕуЃЌНЋ![]() би
би![]() елЕўЕУЕНШчЭМЃЈ2ЃЉЫљЪОЕФШ§РтзЖ
елЕўЕУЕНШчЭМЃЈ2ЃЉЫљЪОЕФШ§РтзЖ![]() ЃЌШєШ§РтзЖ
ЃЌШєШ§РтзЖ![]() ЕФЭтНгЧђЕФАыОЖЮЊ
ЕФЭтНгЧђЕФАыОЖЮЊ![]() ЃЌдђ
ЃЌдђ![]() _________.
_________.
ЭМЃЈ1ЃЉ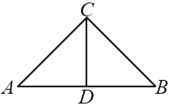 ЭМЃЈ2ЃЉ
ЭМЃЈ2ЃЉ 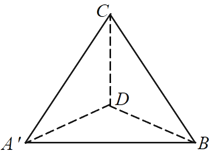
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉЃНЃЈ1ЉsinxЃЉex.
ЃЈ1ЃЉЧѓfЃЈxЃЉдкЧјМфЃЈ0ЃЌІаЃЉЕФМЋжЕЃЛ
ЃЈ2ЃЉжЄУїЃККЏЪ§gЃЈxЃЉЃНfЃЈxЃЉЉsinxЉ1дкЧјМфЃЈЉІаЃЌІаЃЉгаЧвжЛга3ИіСуЕуЃЌЧвжЎКЭЮЊ0.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com