练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若向量＝(cosa,sina)，＝(cosb,sinb)，则与一定满足   （    ）

    A．与的夹角等于a－b  B．⊥  C．∥ D．(＋)⊥(－)

    D


    解析:

    ＋＝(cosa＋cosb,sina＋sinb)，－＝(cosa＋cosb,sina－sinb)，∴(＋)·(－)＝cos2a－cos2b＋sin2a－sin2b＝0，∴(＋)⊥(－)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：河北省冀州中学2010－2011学年高一下学期期末考试数学文科试题(A卷) 题型：044

    在锐角三角形ABC中，已知内角A、B、C所对的边分别为a、b、c，且(tanA－tanB)＝1＋tanA·tanB且a2－ab＝c2－b2，

    (1)求A、B、C的大小；

    (2)若向量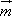＝(sinA，cosA)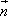，＝(cosB，sinB)，求|3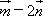|的值．

    查看答案和解析>>

    科目：高中数学 来源：2008届宁夏银川一中高三年级第五次月考测试、数学试卷(理科) 题型：044

    在△ABC中，设内角A、B、C的对边分别为a、b、c，向量＝(cosA，sinA)，＝，若＝2．

    (Ⅰ)求角A的大小；

    (Ⅱ)若，且c＝a，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知A、B、C为三个锐角，且A＋B＋C＝π.若向量＝(2－2sinA，cosA＋sinA)与向量＝(cosA－sinA，1＋sinA)是共线向量.（Ⅰ）求角A；（Ⅱ）求函数y＝2sin2B＋cos的最大值.

    　

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知A、B、C为三个锐角，且A+B+C＝π.若向量＝(2-2sinA，cosA+sinA)与向量＝(cosA-sinA，1+sinA)是共线向量.（Ⅰ）求角A；（Ⅱ）求函数y＝2sin2B+cos的最大值.
    　

    查看答案和解析>>

    同步练习册答案