
(10分)某运动员射击一次所得环数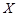 的分布如下:
的分布如下:
|
|
0~6 |
7 |
8 |
9 |
10 |
|
|
0 |
|
|
|
|
现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为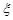 .
.
(I)求该运动员两次都命中7环的概率
(II)求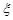 的分布列
的分布列
(III)求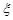 的数学期望
的数学期望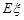
(I) 0.04
(II)

(III) 9.07
【解析】本试题主要考查了独立事件概率的乘法公式好分布列的求解,以及期望公式的的综合运用。
(1)中,利用两次都命中事件同时发生的概率乘法公式得到
(2)中,因为由题意可知ξ可能取值为7、8、9、10,那么分别得到各个取值的概率值,得到分布列。
(3)利用期望公式求解期望值。
解:(I)由题意知运动员两次射击是相互独立的,根据相互独立事件同时发生的概率得到,该运动员两次都命中7环的概率为P=0.2×0.2=0.04
(II)ξ可能取值为7、8、9、10
P(ξ=7)=0.04 P(ξ=8)=2×0.2×0.3+0.32=0.21
P(ξ=9)=2×0.2×0.3+2×0.3×0.3+0.32=0.39
P(ξ=10)=2×0.2×0.2+2×0.3×0.2+2×0.3×0.2+0.22=0.36
∴ξ的分布列为

∴ξ的数学期望为Eξ=7×0.04+8×0.21+9×0.39+10×0.36=9.07


科目:高中数学 来源:2011届广东省高三高考全真模拟试卷数学理卷二 题型:解答题
.(本小题满分12分)第16届亚运会将于2010年11月在广州市举行,射击队运动 员们正在积极备战. 若某运动员每次射击成绩为10环的概率为
员们正在积极备战. 若某运动员每次射击成绩为10环的概率为 . 求该运动员在5次射击中,(1)恰有3次射击成绩为10环的概率;
. 求该运动员在5次射击中,(1)恰有3次射击成绩为10环的概率;
(2)至少有3次射击成绩为10环的概率;
(3)记“射击成绩为10环的次数”为 ,求
,求 .(结果
.(结果 用分数表示)
用分数表示)
查看答案和解析>>
科目:高中数学 来源:2010年江西省四校联考高二上学期期中考试数学文卷 题型:解答题
(本小题满分12分)某射击运动员在一次射击中,命中10环、9环、8环、7环的概率分别为0.2、0.35、0.2、0.15。求此运动员
(1)在一次射击中,命中10环或9环的概率。
(2)在一次射击中,命中环数小于8环的概率。
(3)在两次射击中,至少有一次击中10环的概率。
查看答案和解析>>
科目:高中数学 来源:2009-2010学年广州市七区联考高二数学(理)下学期期末监测 题型:解答题
(本小题满分12分)
第16届亚运会将于今年11月在我市举行,射击队运动员们正在积极备战. 若某运动员每次射击成绩为10环的概率为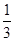 . 求该运动员在5次射击中,
. 求该运动员在5次射击中,
(1)恰有3次射击成绩为10环的概率;
(2)至少有3次射击成绩为10环的概率;
(3)射击成绩为10环的均值(数学期望).
(结果用分数表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com