
【题目】如图,在四棱锥![]() 中,
中,![]() ∥AB,
∥AB,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,E是
,E是![]() 的中点.
的中点.
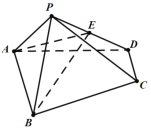
(1)求证:![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)通过证明![]() 和
和![]() ,得
,得![]() 平面
平面![]() ,从而即可得到本题答案;
,从而即可得到本题答案;
(2)以M点为原点,![]() 为x轴,
为x轴,![]() 为y轴,以过点M且垂直平面ABCD的方向为z轴,建立空间直角坐标系,分别求出平面ABE和平面PBE的法向量,然后套用公式即可得到本题答案.
为y轴,以过点M且垂直平面ABCD的方向为z轴,建立空间直角坐标系,分别求出平面ABE和平面PBE的法向量,然后套用公式即可得到本题答案.
(1)证明:如图,设M是![]() 的中点,连接
的中点,连接![]() ,
,
在梯形![]() 中,由已知易得
中,由已知易得![]() ,
,
在![]() 中,
中,![]() ,则
,则![]() ,
,
![]() 与
与![]() 是平面
是平面![]() 内的两条相交直线,
内的两条相交直线,
所以![]() 平面
平面![]() ,而
,而![]() 在平面
在平面![]() 内,
内,
所以![]() ;
;
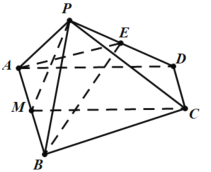
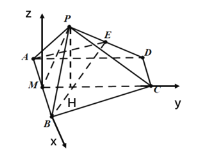
(2)解:作PH垂直于MC,垂足为H,以M点为原点,![]() 为x轴,
为x轴,![]() 为y轴,以过点M且垂直平面ABCD的方向为z轴,建立空间直角坐标系.
为y轴,以过点M且垂直平面ABCD的方向为z轴,建立空间直角坐标系.
在![]() 中,因为
中,因为![]() ,
,![]() ,所以
,所以![]() ,则
,则![]() ,
,
易知![]() ,又
,又![]() ,所以
,所以![]() ,即
,即![]() 为直角三角形,
为直角三角形,
易得![]() ,
,
所以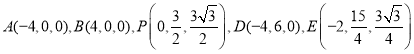
因为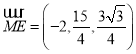 ,
,
所以平面![]() 的一个法向量是
的一个法向量是![]() ,
,
又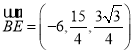 ,
,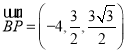 ,
,
所以平面![]() 的一个法向量是
的一个法向量是![]() ,
,
![]() ,
,
由图可知,二面角![]() 为锐角,所以二面角
为锐角,所以二面角![]() 的余弦值是
的余弦值是![]() .
.


科目:高中数学 来源: 题型:
【题目】2020年3月,国内新冠肺炎疫情得到有效控制,人们开始走出家门享受春光.某旅游景点为吸引游客,推出团体购票优惠方案如下表:
购票人数 | 1~50 | 51~100 | 100以上 |
门票价格 | 13元/人 | 11元/人 | 9元/人 |
两个旅游团队计划游览该景点.若分别购票,则共需支付门票费1290元;若合并成个团队购票,则需支付门票费990元,那么这两个旅游团队的人数之差为( )
A.20B.25C.30D.40
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称,旨在积极发展我国与沿线国家经济合作关系,共同打造政治互信、经济融合、文化包容的命运共同体.自2015年以来,“一带一路”建设成果显著.如图是2015—2019年,我国对“一带一路”沿线国家进出口情况统计图,下列描述错误的是( )
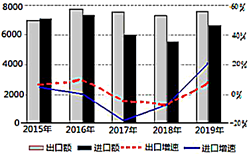
A.这五年,出口总额之和比进口总额之和大
B.这五年,2015年出口额最少
C.这五年,2019年进口增速最快
D.这五年,出口增速前四年逐年下降
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解高中学生对数学课是否喜爱是否和性别有关,随机调查220名高中学生,将他们的意见进行了统计,得到如下的![]() 列联表.
列联表.
喜爱数学课 | 不喜爱数学课 | 合计 | |
男生 | 90 | 20 | 110 |
女生 | 70 | 40 | 110 |
合计 | 160 | 60 | 220 |
(1)根据上面的列联表判断,能否有![]() 的把握认为“喜爱数学课与性别”有关;
的把握认为“喜爱数学课与性别”有关;
(2)为培养学习兴趣,从不喜爱数学课的学生中进行进一步了解,从上述调查的不喜爱数学课的人员中按分层抽样抽取6人,再从这6人中随机抽出2名进行电话回访,求抽到的2人中至少有1名“男生”的概率.
参考公式: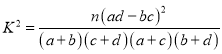 .
.
P( | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假如你的公司计划购买台机器,该种机器使用三年后即被淘汰,在购进机器时,可以一次性额外购买几次维修服务,每次维修服务费用200元,另外实际维修一次还需向维修人员支付小费,小费每次50元,在机器使用期间,如果维修次数超过购机时购买的维修服务次数,则每维修一次需支付维修服务费用500元,无需支付小费,现需决策在购买机器时应同时一次性购买几次维修服务,为此搜集并整理了100台这种机器在三年使用期内的维修次数,得下面统计表:
维修次数 | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 20 | 30 | 30 | 10 |
记![]() 表示1台机器在三年使用期内的维修次数,
表示1台机器在三年使用期内的维修次数,![]() 表示1台机器在维修上所需的费用(单位:元),
表示1台机器在维修上所需的费用(单位:元),![]() 表示购机的同时购买的维修服务次数.
表示购机的同时购买的维修服务次数.
(1)若![]() ,求
,求![]() 与
与![]() 的函数解析式.
的函数解析式.
(2)若要求“维修次数不大于![]() ”的频率不小于0.8,求
”的频率不小于0.8,求![]() 的值.
的值.
(3)假设这100台机器在购机的同时每台都购买10次维修服务,或每台都购买11次维修服务,分别计算这100台机器在维修上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买10次还是11次维修服务?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店举行促销反馈活动,顾客购物每满200元,有一次抽奖机会(即满200元可以抽奖一次,满400元可以抽奖两次,依次类推).抽奖的规则如下:在一个不透明口袋中装有编号分别为1,2,3,4,5的5个完全相同的小球,顾客每次从口袋中摸出一个小球,共摸三次,每次摸出的小球均不放回口袋,若摸得的小球编号一次比一次大(如1,2,5),则获得一等奖,奖金40元;若摸得的小球编号一次比一次小(如5,3,1),则获得二等奖,奖金20元;其余情况获得三等奖,奖金10元.
(1)某人抽奖一次,求其获奖金额X的概率分布和数学期望;
(2)赵四购物恰好满600元,假设他不放弃每次抽奖机会,求他获得的奖金恰好为60元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年国庆节假期期间,某商场为掌握假期期间顾客购买商品人次,统计了10月1日7:00-23:00这一时间段内顾客0这一时间段内顾客购买商品人次,统计发现这一时间段内顾客购买商品共5000人次顾客购买商品时刻的频率分布直方图如下图所示,其中时间段7:00 11:00,11:00 15:00,15:00 ~19:00,19:00~23:00,依次记作[7,11),[11,15),[15,19),[19,23].
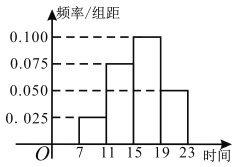
(1)求该天顾客购买商品时刻的中位数t与平均值![]() (同一组中的数据用该组区间的中点值代表);
(同一组中的数据用该组区间的中点值代表);
(2)现从10月1日在该商场购买商品的顾客中随机抽取100名顾客,经统计有男顾客 40人,其中10人购物时刻在[19,23](夜晚),女顾客60人,其中50人购物时刻在[7,19)(白天),根据提供的统计数据,完成下面的2×2列联表,并判断是否有90%的把握认为“男顾客更喜欢在夜晚购物”?
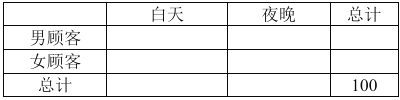
附:![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com