
【题目】命题![]() :函数
:函数![]() 的两个零点分别在区间
的两个零点分别在区间![]() 和
和![]() 上;命题
上;命题![]() :函数
:函数![]() 有极值.若命题
有极值.若命题![]() ,
,![]() 为真命题的实数
为真命题的实数![]() 的取值集合分别记为
的取值集合分别记为![]() ,
,![]() .
.
(1)求集合![]() ,
,![]() ;
;
(2)若命题“![]() 且
且![]() ”为假命题,求实数
”为假命题,求实数![]() 的取值范围.
的取值范围.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】定义一:对于一个函数![]() ,若存在两条距离为
,若存在两条距离为![]() 的直线
的直线![]() 和
和![]() ,使得
,使得![]() 时,
时,![]() 恒成立,则称函数
恒成立,则称函数![]() 在
在![]() 内有一个宽度为
内有一个宽度为![]() 的通道.
的通道.
定义二:若一个函数![]() 对于任意给定的正数
对于任意给定的正数![]() ,都存在一个实数
,都存在一个实数![]() ,使得函数
,使得函数![]() 在
在![]() 内有一个宽度为
内有一个宽度为![]() 的通道,则称
的通道,则称![]() 在正无穷处有永恒通道.
在正无穷处有永恒通道.
下列函数①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() . 其中在正无穷处有永恒通道的函数序号是 .
. 其中在正无穷处有永恒通道的函数序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了茎叶图:则下列结论中表述不正确的是
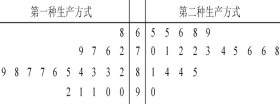
A. 第一种生产方式的工人中,有75%的工人完成生产任务所需要的时间至少80分钟
B. 第二种生产方式比第一种生产方式的效率更高
C. 这40名工人完成任务所需时间的中位数为80
D. 无论哪种生产方式的工人完成生产任务平均所需要的时间都是80分钟.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F是拋物线C:y2=2px(p>0)的焦点,点M(x0,1)在C上,且|MF|=![]() .
.
(1)求p的值;
(2)若直线l经过点Q(3,-1)且与C交于A,B(异于M)两点,证明:直线AM与直线BM的斜率之积为常数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现计划用两张铁丝网在一片空地上围成一个梯形养鸡场![]() ,
,![]() ,
,![]() ,已知
,已知![]()
![]() 两段是由长为
两段是由长为![]() 的铁丝网折成,
的铁丝网折成,![]()
![]() 两段是由长为
两段是由长为![]() 的铁丝网折成.设上底
的铁丝网折成.设上底![]() 的长为
的长为![]() ,所围成的梯形面积为
,所围成的梯形面积为![]() .
.
(1)求S关于x的函数解析式,并求x的取值范围;
(2)当x为何值时,养鸡场的面积最大?最大面积为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A. 命题“![]() ”的否定是“
”的否定是“![]() ”
”
B. 命题“![]() 为真”是命题“
为真”是命题“![]() 为真”的必要不充分条件
为真”的必要不充分条件
C. 若“![]() ,则
,则![]() ”的否命题为真
”的否命题为真
D. 若实数![]() ,则满足
,则满足![]() 的概率为
的概率为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A. 命题“![]() ”的否定是“
”的否定是“![]() ”
”
B. 命题“![]() 为真”是命题“
为真”是命题“![]() 为真”的必要不充分条件
为真”的必要不充分条件
C. 若“![]() ,则
,则![]() ”的否命题为真
”的否命题为真
D. 若实数![]() ,则满足
,则满足![]() 的概率为
的概率为![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com