
【题目】设两个向量![]() ,
,![]() 满足|
满足|![]() |=2,|
|=2,|![]() |=1,
|=1,![]() ,
,![]() 的夹角为60°,若向量2t
的夹角为60°,若向量2t![]() 7
7![]() 与向量
与向量![]() t
t![]() 的夹角为钝角,求实数t的取值范围.
的夹角为钝角,求实数t的取值范围.
科目:高中数学 来源: 题型:
【题目】已知函数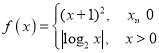 ,若方程f(x)=a有四个不同的解x1,x2,x3,x4,且x1<x2<x3<x4,则
,若方程f(x)=a有四个不同的解x1,x2,x3,x4,且x1<x2<x3<x4,则![]() 的取值范围为( )
的取值范围为( )
A. (﹣1,+∞)B. (﹣1,1]C. (﹣∞,1)D. [﹣1,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=(-x2+ax)ex(x∈R).
(1)当a=2时,求函数f(x)的单调区间;
(2)若函数f(x)在(-1,1)上单调递增,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱柱![]() 中,
中,![]() 为
为![]() 的中点,点
的中点,点![]() 在侧棱
在侧棱![]() 上,
上,![]() 平面
平面![]()
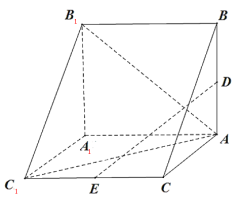
(1) 证明:![]() 是
是![]() 的中点;
的中点;
(2) 设![]() ,四边形
,四边形![]() 为边长为4正方形,四边形
为边长为4正方形,四边形![]() 为矩形,且异面直线
为矩形,且异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,求该三棱柱
,求该三棱柱![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某社区居民有无收看“奥运会开幕式”,某记者分别从某社区60~70岁,40~50岁,20~30岁的三个年龄段中的160人,240人,x人中,采用分层抽样的方法共抽查了30人进行调查,若在60~70岁这个年龄段中抽查了8人,那么x为( ) .
A. 90 B. 120 C. 180 D. 200
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过右焦点
,过右焦点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,分别交椭圆
,分别交椭圆![]() 于
于![]() 和
和![]() 四点.设
四点.设![]() 的中点为
的中点为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 是否经过定点?若是,求出定点坐标;若否,请说明理由.
是否经过定点?若是,求出定点坐标;若否,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某校高二![]() 名学生的体能情况,随机抽查部分学生,测试
名学生的体能情况,随机抽查部分学生,测试![]() 分钟仰卧起坐的成绩(次数),将数据整理后绘制成如图所示的频率分布直方图,根据统计图的数据,下列结论错误的是( )
分钟仰卧起坐的成绩(次数),将数据整理后绘制成如图所示的频率分布直方图,根据统计图的数据,下列结论错误的是( )
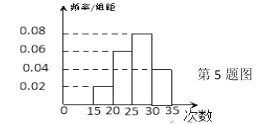
A.该校高二学生![]() 分钟仰卧起坐的次数超过
分钟仰卧起坐的次数超过![]() 次的人数约有
次的人数约有![]() 人
人
B.该校高二学生![]() 分钟仰卧起坐的次数少于
分钟仰卧起坐的次数少于![]() 次的人数约有
次的人数约有![]() 人
人
C.该校高二学生![]() 分钟仰卧起坐的次数的中位数为
分钟仰卧起坐的次数的中位数为![]() 次
次
D.该校高二学生![]() 分钟仰卧起坐的次数的众数为
分钟仰卧起坐的次数的众数为![]() 次
次
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,下顶点为
,下顶点为![]() ,椭圆
,椭圆![]() 的离心率是
的离心率是![]() ,
,![]() 的面积是
的面积是![]() .
.
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(异于
两点(异于![]() 点),若直线
点),若直线![]() 与直线
与直线![]() 的斜率之和为1,证明:直线
的斜率之和为1,证明:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com