
分析 (1)根据判别式分类讨论求出不等式的解集,
(2)分离参数,根据基本不等式即可求出a的取值范围.
解答 解:(1)△=a2-4,
①当△>0,即a>2或a<-2时,不等式的解集为(-∞,$\frac{-a-\sqrt{{a}^{2}-4}}{2}$)∪($\frac{-a+\sqrt{{a}^{2}-4}}{2}$,+∞),
②当△=0,即a=2或-2时,
当a=2时,不等式的解集为(-∞,-1)∪(-1,+∞);
当a=-2时,不等式的解集为(-∞,1)∪(1,+∞);
③当△<0,即当-2<a<2时,解集为R.
综上,①当a>2或a<-2时,不等式的解集为(-∞,$\frac{-a-\sqrt{{a}^{2}-4}}{2}$)∪($\frac{-a+\sqrt{{a}^{2}-4}}{2}$,+∞);
②当a=2时,不等式的解集为(-∞,-1)∪(-1,+∞);
③当a=-2时,不等式的解集为(-∞,1)∪(1,+∞);
④当-2<a<2时,解集为R.
(2)当x>0时,由x2+ax+1≥0得a≥-(x+$\frac{1}{x}$)=-2$\sqrt{x•\frac{1}{x}}$=-2,当且仅当x=1时取等号.
故a的取值范围为[-2,+∞)
点评 本题考查了一元二次不等式的解法和基本不等式的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π+6}{4}$ | B. | $\frac{3π+4}{4}$ | C. | π+1 | D. | $\frac{3π+3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
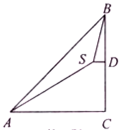 如图,在山底A处测得山顶B的仰角∠CAB=45°,沿倾斜角为30°的斜坡AS走2000米至S点,又测得山顶∠DSB=75°,则山高BC为2000米.
如图,在山底A处测得山顶B的仰角∠CAB=45°,沿倾斜角为30°的斜坡AS走2000米至S点,又测得山顶∠DSB=75°,则山高BC为2000米.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学偏差x | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
| 物理偏差y | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{20π}{3}$ | B. | $\frac{20\sqrt{5}π}{3}$ | C. | 20$\sqrt{5}$π | D. | $\frac{100π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com