
����Ŀ��Ϊӭ��2016�ꡰ���ĵ�����ij����̨�ٰ�½�������������Ⱥ�ش�����ѡ���⣬����A������ѡ�����B���ĸ�ѡ�ÿ��ֻ��һ��ѡ������ȷ�ģ���ȷ�ش�����A�ɻ�1ǧԪ����ȷ�ش�����B�ɻ�2ǧԪ����涨�������߿�����ѡ��ش������˳�������һ������ش���ȷ����������⣬����ò����߲½����ֹ������ij�������ڻش�����ǰ��ѡ��ÿ�����ÿ��ѡ��Ļ����ǵȿ��ܵģ�
��������ò������Ȼش�����A������ǡ�û�ý���1ǧԪ�ĸ��ʣ�
������ȷ�����ֻش������˳����ʹ�ò�����������ֵ�ϴ�
���𰸡��⣺��������¶�����A�ĸ���P1= ![]() ������¶�����B�ĸ���P2=
������¶�����B�ĸ���P2= ![]() ��
��
��������Ȼش�����A����ǡ�û�ý���1ǧԪΪ�¼�M��
��P��M��=P1��1��P2��= ![]() =
= ![]() ��
��
���������Ȼش�����A����ǡ�û�ý���1ǧԪ�ĸ���Ϊ ![]() ��
��
�������ش������˳�������֣��ֱ��������£�
���Ȼش�����A���ٻش�����B���������ο�ȡ0��1000��3000��
��P����=0��=1��P1= ![]() ��
��
P����=1000��=P1��1��P2��= ![]() ��
��
P����=3000��=P1P2= ![]() =
= ![]() ��
��
��E��=0�� ![]() +1000��
+1000�� ![]() +3000��
+3000�� ![]() =500��
=500��
���Ȼش�����B���ٻش�����A���������ǣ���ȡ0��2000��3000��
��P����=0��=1��P2=1�� ![]() ��
��
P����=2000��=��1��P1��P2= ![]() =
= ![]() ��
��
P����=3000��=P2P1= ![]() ��
��
��E��=0�� ![]() +2000��
+2000�� ![]() +3000��
+3000�� ![]() ��583��
��583��
���Ȼش�����B���ٻش�����A����ʹ�ò�����������ֵ�ϴ�
����������������¶�����A�ĸ���P1= ![]() ������¶�����B�ĸ���P2=
������¶�����B�ĸ���P2= ![]() �����ø��ʵij˷���ʽ����������Ȼش�����A��ǡ�û�ý���1ǧԪ�ĸ��ʣ��������ش������˳�������֣��Ȼش�����A���ٻش�����B���Ȼش�����B���ٻش�����A��������������µĻ�ʤ�����������бȽϣ��������ۣ�
�����ø��ʵij˷���ʽ����������Ȼش�����A��ǡ�û�ý���1ǧԪ�ĸ��ʣ��������ش������˳�������֣��Ȼش�����A���ٻش�����B���Ȼش�����B���ٻش�����A��������������µĻ�ʤ�����������бȽϣ��������ۣ�
�����㾫����������Ĺؼ�����������ɢ�������������ֲ��е����֪ʶ���������������Ʒ����������У������������X����ȡ��ֵ�����ǿ���һ������һһ�г����������������������ɢ�������������ɢ����������ķֲ��У�һ���,����ɢ���������X����ȡ��ֵΪx1,x2,.....,xi,......,xn��Xȡÿһ��ֵ xi(i=1,2,......���ĸ���P(��=xi����Pi����Ʊ�Ϊ��ɢ���������X �ĸ��ʷֲ�����Ʒֲ��У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1��������ʽ![]() ���������ʵ��
���������ʵ��![]() �����ֵ��
�����ֵ��
��2����![]() ʱ������
ʱ������![]() ����㣬��ʵ��
����㣬��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P1��P2������P6Ϊ��λԲ����ʱ����ȷֲ��������㣮����ѡ����������ͬ�㹹��һ�������Σ��Ǹ������ε����Ϊ�������S��
��1����S��![]() �ĸ��ʣ�
�ĸ��ʣ�
��2����S�ķֲ��м���ѧ����E(S)��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x��=x2��a|x��1|+b��a��0��b����1��
��1����b=0��a��2����f��x��������[0��2]�ڵ���Сֵm��a����
��2����f��x��������[0��2]�ڲ�ͬ�����ǡ������������������[0��1������1��2]�ڸ�һ������a��b��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С�l2����
��ͼ����ֱ������ABC��A1B1C1�У���BAC=90�㣬AB=AC=AA1=1���ӳ�A1C1����P��ʹC1P��A1C1������AP����CC1��D��
������֤��PB1��ƽ��BDA1��
����������A��A1D��B��ƽ��ǵ�����ֵ��
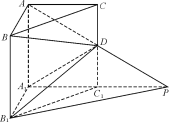
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������̨ABO��A1B1O1�У�����AOO1A1�����OBB1O1��ȫ�ȵ�ֱ�����Σ���OO1��OB��OO1��OA��ƽ��AOO1A1��ƽ��OBB1O1 �� OB=3��O1B1=1��OO1= ![]() ��
�� 
��1��֤����AB1��BO1��
��2����ֱ��AO1��ƽ��AOB1���ɵĽǵ�����ֵ��
��3��������O��AB1��O1������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=ax2��lnx��a��R��
��1����a=1ʱ������y=f��x���ĵ������䣻
��2����x�ʣ�0��1]��|f��x��|��1���������a��ȡֵ��Χ��
��3����a= ![]() ��֤����ex��1f��x����x��
��֤����ex��1f��x����x��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=ax2��lnx��a��R��
��1����a=1ʱ������y=f��x���ĵ������䣻
��2����x�ʣ�0��1]��|f��x��|��1���������a��ȡֵ��Χ��
��3����a= ![]() ��֤����ex��1f��x����x��
��֤����ex��1f��x����x��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com