
定义在R上的函数 ,其图象是连续不断的,如果存在非零常数
,其图象是连续不断的,如果存在非零常数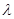 (
(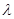 ∈R,使得对任意的x
∈R,使得对任意的x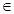 R,都有f(x+
R,都有f(x+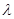 )=
)=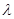 f(x),则称y=f(x)为“倍增函数”,
f(x),则称y=f(x)为“倍增函数”,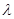 为“倍增系数”,下列命题为真命题的是____(写出所有真命题对应的序号).
为“倍增系数”,下列命题为真命题的是____(写出所有真命题对应的序号).
①若函数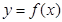 是倍增系数
是倍增系数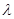 =-2的倍增函数,则
=-2的倍增函数,则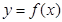 至少有1个零点;
至少有1个零点;
②函数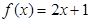 是倍增函数,且倍增系数
是倍增函数,且倍增系数 =1;
=1;
③函数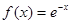 是倍增函数,且倍增系数
是倍增函数,且倍增系数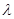 ∈(0,1);
∈(0,1);
④若函数 是倍增函数,则
是倍增函数,则
①③④
【解析】∵函数y=f(x)是倍增系数λ=-2的倍增函数,∴f(x-2)=-2f(x),
当x=0时,f(-2)+2f(0)=0,若f(0),f(-2)任一个为0,函数f(x)有零点.
若f(0),f(-2)均不为零,则f(0),f(-2)异号,
由零点存在定理,在(-2,0)区间存在x0,f(x0)=0,即y=f(x)至少有1个零点,故①正确;
∵f(x)=2x+1是倍增函数,∴2(x+λ)+1=λ(2x+1),∴ ,故②不正确;
,故②不正确;
∵ 是倍增函数,∴
是倍增函数,∴ ,∴
,∴ ,故③正确;
,故③正确;
∵f(x)=sin(2ωx)(ω>0)是倍增函数,∴sin[2ω(x+λ)]=λsin(2ωx),
∴ .故④正确.故答案为:①③④.
.故④正确.故答案为:①③④.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| b | a |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com