【题目】设命题
对任意实数
，不等式
恒成立；命题
方程
表示焦点在
轴上的双曲线．
（1）若命题
为真命题，求实数
的取值范围；
（2）若命题：“
”为真命题，且“
”为假命题，求实数
的取值范围．
【答案】（1）
；（2）
.
【解析】
试题分析：（1）由于双曲线焦点在
轴上，所以
，解得；（2）不等式
恒成立，等价于判别式为非正数，解得
.若
或
真、
且
假，则这两个命题一真一假.分别求出
假
真和
真
假时
的取值范围，取并集得到
的取值范围.
试题解析：
（1）因为方程
表示焦点在
轴上的双曲线.
∴，得
；∴当时，
为真命题，………………………3分
（2）∵不等式恒成立，∴
，∴，
∴当时，
为真命题．．．．．．．．．．．．．．．．．．．．．．．．．．．．6分
∵
为假命题，
为真命题，∴
一真一假；．．．．．．．．．．．．．．．．．．．．．．．7分
①当
真
假
，②当
假
真
无解
综上，
的取值范围是．．．．．．．．．．．．．．．．．．．．．．．．．．．．10分
备战中考寒假系列答案科目：高中数学 来源： 题型：
【题目】已知椭圆
： 
的左，右焦点分别为
， 
，离心率为
， 
是椭圆
上的动点，当
时， 
的面积为
.
（1）求椭圆
的标准方程；
（2）若过点
的直线交椭圆
于
， 
两点，求
面积的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
（
），
.
(1)若对任意的
，
，都有
恒成立，试求m的取值范围；
(2)用
表示m，n中的最小值，设函数
（
），讨论关于x的方程
的实数解的个数.
查看答案和解析>>
科目：高中数学 来源： 题型：
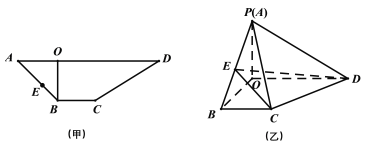
【题目】如图甲所示，
是梯形
的高，
，
，
，先将梯形沿
折起如图乙所示的四棱锥
，使得
.
（1）在棱
上是否存在一点
，使得
平面
？若存在，请求出
的值，若不存在，请说明理由;
（2）点
是线段
上一动点，当直线
与
所成的角最小时，求二面角
的余弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司为了解用户对其产品的满意度，从某地区随机调查了100个用户，得到用户对产品的满意度评分频率分布表如下：
组别 | 分组 | 频数 | 频率 |
第一组 |
| 10 | 0.1 |
第二组 |
| 20 | 0.2 |
第三组 |
| 40 | 0.4 |
第四组 |
| 25 | 0.25 |
第五组 |
| 5 | 0.05 |
合计 | 100 | 1 |
（1）根据上面的频率分布表，估计该地区用户对产品的满意度评分超过70分的概率；
（2）请由频率分布表中数据计算众数、中位数，平均数，根据样本估计总体的思想，若平均分低于75分，视为不满意.判断该地区用户对产品是否满意？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图是正方体的平面展开图，在这个正方体中；
（1）BM与ED平行；（2）CN与BE是异面直线；（3）CN与BM所成角为60°；（4）CN与AF垂直. 以上四个命题中，正确命题的序号是（ ）
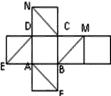
A.（1）（2）（3）B.（2）（4）C.（3）（4）D.（3）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）＝sin（ωx＋θ），其中ω＞0，θ∈（0，
），
＝
＝0，（x1≠x2），｜x2－x1｜min＝，f（x）＝f（
－x），将函数f（x）的图象向左平移
个单位长度得到函数g（x）的图象，则函数g（x）的单调递减区间是
A. [kπ－，kπ＋]（k∈Z） B. [kπ，kπ＋]（k∈Z）
C. [kπ＋，kπ＋
]（k∈Z） D. [kπ＋
，kπ＋
]（k∈Z）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
