
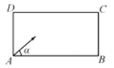
【题目】台球运动已有五、六百年的历史,参与者用球杆在台上击球.若和光线一样,台球在球台上碰到障碍物后也遵从反射定律如图,有一张长方形球台ABCD,![]() ,现从角落A沿角
,现从角落A沿角![]() 的方向把球打出去,球经2次碰撞球台内沿后进入角落C的球袋中,则
的方向把球打出去,球经2次碰撞球台内沿后进入角落C的球袋中,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.1D.
C.1D.![]()
科目:高中数学 来源: 题型:
【题目】对一个量用两种方法分别算一次,由结果相同而构造等式,这种方法称为“算两次”的思想方法.利用这种方法,结合二项式定理,可以得到很多有趣的组合恒等式.
(1)根据恒等式![]() 两边
两边![]() 的系数相同直接写出一个恒等式,其中
的系数相同直接写出一个恒等式,其中![]() ;
;
(2)设![]() ,利用上述恒等式证明:
,利用上述恒等式证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,我国大力发展新能源汽车工业,新能源汽车(含电动汽车)销量已跃居全球首位.某电动汽车厂新开发了一款电动汽车.并对该电动汽车的电池使用情况进行了测试,其中剩余电量y与行驶时问![]() (单位:小时)的测试数据如下表:
(单位:小时)的测试数据如下表:

(1)根据电池放电的特点,剩余电量y与行驶时间![]() 之间满足经验关系式:
之间满足经验关系式:![]() ,通过散点图可以发现y与
,通过散点图可以发现y与![]() 之间具有相关性.设
之间具有相关性.设![]() ,利用表格中的前8组数据求相关系数r,并判断是否有99%的把握认为
,利用表格中的前8组数据求相关系数r,并判断是否有99%的把握认为![]() 与
与![]() 之间具有线性相关关系;(当相关系数r满足
之间具有线性相关关系;(当相关系数r满足![]() 时,则认为有99%的把握认为两个变量具有线性相关关系)
时,则认为有99%的把握认为两个变量具有线性相关关系)
(2)利用![]() 与
与![]() 的相关性及表格中前8组数据求出
的相关性及表格中前8组数据求出![]() 与
与![]() 之间的回归方程;(结果保留两位小数)
之间的回归方程;(结果保留两位小数)
(3)如果剩余电量不足0.8,电池就需要充电.从表格中的10组数据中随机选出8组,设X表示需要充电的数据组数,求X的分布列及数学期望.
附:相关数据:![]() .
.
表格中前8组数据的一些相关量:![]() ,
,![]() ,
,
相关公式:对于样本![]() ,其回归直线
,其回归直线![]() 的斜率和戗距的最小二乘估计公式分别为:
的斜率和戗距的最小二乘估计公式分别为: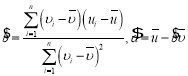 ,
,
相关系数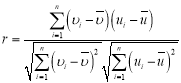 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校李老师本学期任高一A班、B班两个班数学课教学,两个班都是50个学生,下图反映的是两个班在本学期5次数学检测中的班级平均分对比,根据图表信息,下列不正确的结论是( )

A. A班的数学成绩平均水平好于B班
B. B班的数学成绩没有A班稳定
C. 下次B班的数学平均分高于A班
D. 在第一次考试中,A、B两个班总平均分为78分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】法国数学家庞加是个喜欢吃面包的人,他每天都会购买一个面包,面包师声称自己出售的每个面包的平均质量是1000![]() ,上下浮动不超过50
,上下浮动不超过50![]() .这句话用数学语言来表达就是:每个面包的质量服从期望为1000
.这句话用数学语言来表达就是:每个面包的质量服从期望为1000![]() ,标准差为50
,标准差为50![]() 的正态分布.
的正态分布.
(1)假设面包师的说法是真实的,从面包师出售的面包中任取两个,记取出的两个面包中质量大于1000![]() 的个数为
的个数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)作为一个善于思考的数学家,庞加莱每天都会将买来的面包称重并记录,25天后,得到数据如下表,经计算25个面包总质量为24468![]() .庞加莱购买的25个面包质量的统计数据(单位:
.庞加莱购买的25个面包质量的统计数据(单位:![]() )
)
981 | 972 | 966 | 992 | 1010 | 1008 | 954 | 952 | 969 | 978 |
989 | 1001 | 1006 | 957 | 952 | 969 | 981 | 984 | 952 | 959 |
987 | 1006 | 1000 | 977 | 966 |
尽管上述数据都落在![]() 上,但庞加菜还是认为面包师撒谎,根据所附信息,从概率角度说明理由
上,但庞加菜还是认为面包师撒谎,根据所附信息,从概率角度说明理由
附:
①若![]() ,从X的取值中随机抽取25个数据,记这25个数据的平均值为Y,则由统计学知识可知:随机变量
,从X的取值中随机抽取25个数据,记这25个数据的平均值为Y,则由统计学知识可知:随机变量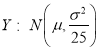
②若![]() ,则
,则![]() ,
,![]() ,
,![]() ;
;
③通常把发生概率在0.05以下的事件称为小概率事件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 的参数方程为
的参数方程为 (t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求![]() 的普通方程和曲线C的直角坐标方程;
的普通方程和曲线C的直角坐标方程;
(2)求曲线C上的点到![]() 距离的最大值及该点坐标.
距离的最大值及该点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的两个焦点分别是
的两个焦点分别是![]() ,直线
,直线![]() :
:![]() 与椭圆交于
与椭圆交于![]() 两点.
两点.
(1)若![]() 为椭圆短轴上的一个顶点,且
为椭圆短轴上的一个顶点,且![]() 是直角三角形,求
是直角三角形,求![]() 的值;
的值;
(2)若![]() ,且
,且![]() ,求证:
,求证:![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com