练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．下列函数中，定义在R上的增函数是（　　）
    A．$y=x-\frac{1}{x}$B．y=lg|x|C．$y=\root{3}{x}$D．$y=\sqrt{x^2}$

    分析 根据题意，对选项中函数的定义域和单调性进行判断即可．

    解答 解：对于A，函数y=x-$\frac{1}{x}$的定义域是{x|x≠0}，不满足题意；
    对于B，函数y=lg|x|的定义域是{x|x≠0}，不满足题意；
    对于C，函数y=$\root{3}{x}$是定义域R上的增函数，满足题意；
    对于D，函数y=$\sqrt{{x}^{2}}$=|x|在定义域R上不是单调函数，不满足题意．
    故选：C．

    点评 本题考查了基本初等函数的定义域和单调性的应用问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    3．不等式$\frac{2x}{3x-1}$＞1的解为（　　）
    A．$（\frac{1}{3}，\frac{1}{2}）$B．$（\frac{1}{2}，1）$C．$（\frac{1}{3}，1）$D．$（-\frac{1}{3}，\frac{1}{2}）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知直线l的极坐标方程为ρsin（θ+$\frac{π}{4}$）=$\sqrt{2}$．
    （1）在极坐标系下写出θ=0和θ=$\frac{π}{2}$时该直线上的两点的极坐标，并画出该直线；
    （2）已知Q是曲线ρ=1上的任意一点，求点Q到直线l的最短距离及此时Q的极坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．已知变量x，y满足约束条件$\left\{\begin{array}{l}x+y≥2\\ x-y≤2\\ 0≤y≤3\end{array}\right.$，若目标函数z=y-ax仅在点（5，3）处取得最小值，则实数a的取值范围为（1，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．在等比数列中，若S10=10，S20=30，则S30等于（　　）
    A．50B．60C．70D．90

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．某校教职工年龄结构分布如表，为了该校未来的发展，学校决定从这些教职工中采用分层抽样方法随机抽取50人参与“教代会”，则应从35岁以下教职工中抽取的人数为（　　）
    年龄（岁）35岁及以下（35，50）50岁以上
    人数（人）220180100
    A．22B．18C．10D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知定点A（7，0），B（1，0），平面上动点P到A点的距离与到B点的距离之比为λ（λ＞0，且为常数）
    （I）求动点P的轨迹方程，并说明方程表示的曲线；
    （II）当λ=2时，记P点的轨迹与y轴交于M、N两点，若过点P做圆C：（x-1）2+y2=1的两条切线l1、l2分别交y轴于H、K两点，在构成三角形的条件下，求$\frac{{{S_△}_{PMN}}}{{{S_{△PHK}}}}$得最大值，并指出取得最大值时的P点坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

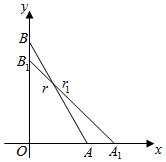    2．如图，长为4的线段AB的两个端点A和B分别在x轴正半轴和y正半轴上滑动，T为AB的中点，∠OAB=75°，当线段AB滑动到A1B1位置时，∠OA1B1=45°．线段在滑动时点T运动到T1点，则点T运动的路程为$\frac{π}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．给出两个命题：
    命题p：关于x的不等式x2+（a-1）x+a2≤0的解集为空集．
    命题q：函数y=（2a2-a）x为增函数．
    分别求出符合下列条件的实数a的范围．
    （1）p∨q为真；
    （2）p∨q为真，p∧q为假．

    查看答案和解析>>

    同步练习册答案