
【题目】如图,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.
(I)证明:CE∥平面PAB;
(II)求直线CE与平面PBC所成角的正弦值

【答案】(I)见解析;(II)![]() .
.
【解析】试题本题主要考查空间点、线、面位置关系,直线与平面所成的角等基础知识,同时考查空间想象能力和运算求解能力。满分15分。
(Ⅰ)取PA中点F,构造平行四边形BCEF,可证明;(Ⅱ)由题意,取BC,AD的中点M,N,可得AD⊥平面PBN,即BC⊥平面PBN,过点Q作PB的垂线,垂足为H,连结MH.可知MH是MQ在平面PBC上的射影,所以∠QMH是直线CE与平面PBC所成的角.依此可在Rt△MQH中,求∠QMH的正弦值.
试题解析:
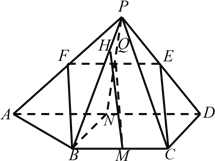
(Ⅰ)如图,设PA中点为F,连接EF,FB.
因为E,F分别为PD,PA中点,所以![]() 且
且![]() ,
,
又因为![]() ,
, ![]() ,所以
,所以![]() 且
且![]() ,
,
即四边形BCEF为平行四边形,所以![]() ,
,
因此![]() 平面PAB.
平面PAB.
(Ⅱ)分别取BC,AD的中点为M,N.连接PN交EF于点Q,连接MQ.
因为E,F,N分别是PD,PA,AD的中点,所以Q为EF中点,
在平行四边形BCEF中,MQ//CE.
由△PAD为等腰直角三角形得PN⊥AD.
由DC⊥AD,N是AD的中点得BN⊥AD.
所以AD⊥平面PBN,
由BC//AD得BC⊥平面PBN,
那么平面PBC⊥平面PBN.
过点Q作PB的垂线,垂足为H,连接MH.
MH是MQ在平面PBC上的射影,所以∠QMH是直线CE与平面PBC所成的角.
设CD=1.
在△PCD中,由PC=2,CD=1,PD=![]() 得CE=
得CE=![]() ,
,
在△PBN中,由PN=BN=1,PB=![]() 得QH=
得QH=![]() ,
,
在Rt△MQH中,QH=![]() ,MQ=
,MQ=![]() ,
,
所以sin∠QMH=![]() ,
,
所以直线CE与平面PBC所成角的正弦值是![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知以M点为圆心的圆![]() 及其上一点
及其上一点![]() .
.

(1)设圆N与y轴相切,与圆M外切,且圆心在直线![]() 上,求圆N的标准方程;
上,求圆N的标准方程;
(2)设平行于OA的直线l与圆M相交于B,C两点且![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年9月,台风“山竹”在沿海地区登陆,小张调查了当地某小区的100户居民由于台风造成的经济损失,将收集到的数据分成五组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 单位:千元
单位:千元![]() ,并作出如下频率分布直方图
,并作出如下频率分布直方图

经济损失不超过4千元 | 经济损失超过4千元 | 合计 | |
捐款超过 500元 | 60 | ||
捐款不超 过500元 | 10 | ||
合计 |
![]() 1
1![]() 台风后居委会号召小区居民为台风重灾区捐款,小张调查的100户居民捐款情况如表格,在表格空白处填写正确数字,并说明是否有
台风后居委会号召小区居民为台风重灾区捐款,小张调查的100户居民捐款情况如表格,在表格空白处填写正确数字,并说明是否有![]() 以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4千元有关?
以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4千元有关?
![]() 2
2![]() 将上述调查得到的频率视为概率,现在从该地区大量受灾居民中,采用随机抽样的方法每次抽取一户居民,连抽3次,记被抽取的3户居民中自身经济损失超过4千元的户数为
将上述调查得到的频率视为概率,现在从该地区大量受灾居民中,采用随机抽样的方法每次抽取一户居民,连抽3次,记被抽取的3户居民中自身经济损失超过4千元的户数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:临界值表:
|
|
|
|
k |
|
|
|
随机变量:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,除
的包裹,除![]() 收费
收费![]() 元之外,超过
元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需再收
计算)需再收![]() 元.
元.
该公司将近![]() 天,每天揽件数量统计如下:
天,每天揽件数量统计如下:
包裹件数范围 |
|
|
|
|
|
包裹件数 (近似处理) |
|
|
|
|
|
天数 |
|
|
|
|
|
(1)某人打算将![]() ,
, ![]() ,
, ![]() 三件礼物随机分成两个包裹寄出,求该人支付的快递费不超过
三件礼物随机分成两个包裹寄出,求该人支付的快递费不超过![]() 元的概率;
元的概率;
(2)该公司从收取的每件快递的费用中抽取![]() 元作为前台工作人员的工资和公司利润,剩余的作为其他费用.前台工作人员每人每天揽件不超过
元作为前台工作人员的工资和公司利润,剩余的作为其他费用.前台工作人员每人每天揽件不超过![]() 件,工资
件,工资![]() 元,目前前台有工作人员
元,目前前台有工作人员![]() 人,那么,公司将前台工作人员裁员
人,那么,公司将前台工作人员裁员![]() 人对提高公司利润是否更有利?
人对提高公司利润是否更有利?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲、乙两品种的棉花中各抽测了25根棉花的纤维长度(单位:mm),得到如图5的茎叶图,整数位为茎,小数位为叶,如27.1mm的茎为27,叶为1.

(1)试比较甲、乙两种棉花的纤维长度的平均值的大小及方差的大小;(只需写出估计的结论,不需说明理由)
(2)将棉花按纤维长度的长短分成七个等级,分级标准如表:

试分别估计甲、乙两种棉花纤维长度等级为二级的概率;
(3)为进一步检验甲种棉花的其它质量指标,现从甲种棉花中随机抽取4根,记![]() 为抽取的棉花纤维长度为二级的根数,求
为抽取的棉花纤维长度为二级的根数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在圆![]() 上任取一点
上任取一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线段,垂足为
轴的垂线段,垂足为![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() ,当点
,当点![]() 在圆上运动时.
在圆上运动时.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设直线![]() 与上述轨迹
与上述轨迹![]() 相交于M、N两点,且MN的中点在直线
相交于M、N两点,且MN的中点在直线![]() 上,求实数k的取值范围.
上,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,过点
中,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为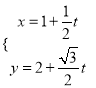 (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 是边长为
是边长为![]() 的正方形,平面
的正方形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
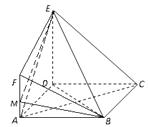
(1)求证:面![]() 面
面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com