
【题目】已知函数![]()
(1)若![]() 在
在![]() 处取得极值,求实数
处取得极值,求实数![]() 的值.
的值.
(2)求函数![]() 的单调区间.
的单调区间.
(3)若![]() 在
在![]() 上没有零点,求实数
上没有零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)单调增区间为
(2)单调增区间为![]() ,单调减区间为
,单调减区间为![]() (3)
(3)![]()
【解析】试题分析:(1)求导![]() ,令
,令![]() 得
得![]() ,再讨论单调性下结论即可;
,再讨论单调性下结论即可;
(2)由![]() ,令
,令![]() 可得增区间,令
可得增区间,令![]() 可得减区间;
可得减区间;
(3)要使![]() 在
在![]() 上没有零点,只需在
上没有零点,只需在![]() 上
上![]() 或
或![]() ,又
,又![]() ,只需在区间
,只需在区间![]() 上,
上, ![]() ,分
,分![]() ,
, ![]() 和
和![]() 三种情况讨论即可.
三种情况讨论即可.
试题解析:
(1)![]() 的定义域为
的定义域为![]() ,且
,且![]() .
.
∵![]() 在
在![]() 处取得极值,
处取得极值,
∴![]() ,解得
,解得![]() 或
或![]() (舍),
(舍),
当![]() 时,
时, ![]() ,
, ![]() ;
;
![]() ,
, ![]() ,
,
∴函数![]() 在
在![]() 处取得极小值,
处取得极小值,
故![]() .
.
(2)![]() .
.
令![]() ,解得
,解得![]() ;
;
令![]() ,解得
,解得![]() ,
,
∴函数![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]()
(3)要使![]() 在
在![]() 上没有零点,只需在
上没有零点,只需在![]() 上
上![]() 或
或![]() ,
,
又![]() ,只需在区间
,只需在区间![]() 上,
上, ![]() .
.
①当![]() 时,
时, ![]() 在区间
在区间![]() 上单调递减,则
上单调递减,则![]() ,
,
解得![]() 与
与![]() 矛盾.
矛盾.
②当![]() 时,
时, ![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
![]() ,
,
解得![]() ,
,
∴![]()
③当![]() 时,
时, ![]() 在区间
在区间![]() 上单调递增,
上单调递增,
![]() ,满足题意,
,满足题意,
综上所述,实数![]() 的取值范围是:
的取值范围是: ![]() .
.


科目:高中数学 来源: 题型:
【题目】《中国好声音(![]()
![]()
![]()
![]() )》是由浙江卫视联合星空传媒旗下灿星制作强力打造的大型励志专业音乐评论节目,于2012年7月13日在浙江卫视播出.每期节目有四位导师参加.导师背对歌手,当每位参赛选手演唱完之前有导师为其转身,则该选手可以选择加入为其转身的导师的团队中接受指导训练.已知某期《中国好声音》中,6位选手唱完后,四位导师为其转身的情况如下表所示:
)》是由浙江卫视联合星空传媒旗下灿星制作强力打造的大型励志专业音乐评论节目,于2012年7月13日在浙江卫视播出.每期节目有四位导师参加.导师背对歌手,当每位参赛选手演唱完之前有导师为其转身,则该选手可以选择加入为其转身的导师的团队中接受指导训练.已知某期《中国好声音》中,6位选手唱完后,四位导师为其转身的情况如下表所示:
导师转身人数(人) | 4 | 3 | 2 | 1 |
获得相应导师转身的选手人数(人) | 1 | 2 | 2 | 1 |
现从这6位选手中随机抽取两人考查他们演唱完后导师的转身情况.
(1)请列出所有的基本事件;
(2)求两人中恰好其中一位为其转身的导师不少于3人,而另一人为其转身的导师不多于2人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() .直角梯形
.直角梯形![]() 通过直角梯形
通过直角梯形![]() 以直线
以直线![]() 为轴旋转得到,且使平面
为轴旋转得到,且使平面![]() 平面
平面![]() .
. ![]() 为线段
为线段![]() 的中点,
的中点, ![]() 为线段
为线段![]() 上的动点.
上的动点.

(1)求证: ![]() ;
;
(2)当点![]() 是线段
是线段![]() 中点时,求二面角
中点时,求二面角![]() 的余弦值;
的余弦值;
(3)是否存在点![]() ,使得直线
,使得直线![]() 平面
平面![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016·北京卷)如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=![]() .
.
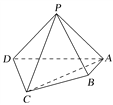
(1)求证:PD⊥平面PAB;
(2)求直线PB与平面PCD所成角的正弦值;
(3)在棱PA上是否存在点M,使得BM∥平面PCD?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点P为圆心的圆经过点A(-1,0)和B(3,4),线段AB的垂直平分线交圆P于点C和D,且|CD|=![]() .
.
(1)求直线CD的方程;
(2)求圆P的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() .
.
(1)求圆心C的坐标及半径r的大小;
(2)已知不过原点的直线l与圆C相切,且在x轴、y轴上的截距相等,求直线l的方程;
(3)从圆外一点![]() 向圆引一条切线,切点为M,O为坐标原点,且
向圆引一条切线,切点为M,O为坐标原点,且![]() ,求点P的轨迹方程.
,求点P的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目,若一名学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.
某学校为了了解高一年级420名学生选考科目的意向,随机选取30名学生进行了一次调查,统计选考科目人数如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有8人 | 8 | 8 | 4 | 2 | 1 | 1 |
选考方案待确定的有6人 | 4 | 3 | 0 | 1 | 0 | 0 | |
女生 | 选考方案确定的有10人 | 8 | 9 | 6 | 3 | 3 | 1 |
选考方案待确定的有6人 | 5 | 4 | 1 | 0 | 0 | 1 |
(Ⅰ)估计该学校高一年级选考方案确定的学生中选考生物的学生有多少人?
(Ⅱ)假设男生、女生选择选考科目是相互独立的.从选考方案确定的8位男生随机选出1人,从选考方案确定的10位女生中随机选出1人,试求该男生和该女生的选考方案中都含有历史科目的概率;
(Ⅲ)从选考方案确定的8名男生随机选出2名,设随机变量两名男生选考方案相同时![]() ,两名男生选考方案不同时
,两名男生选考方案不同时![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com