
【题目】已知圆![]() :
:![]() (
(![]() )与直线
)与直线![]() :
:![]() 相切,设点
相切,设点![]() 为圆上一动点,
为圆上一动点,![]() 轴于
轴于![]() ,且动点
,且动点![]() 满足
满足![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)直线![]() 与直线
与直线![]() 垂直且与曲线
垂直且与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)利用圆![]() 与直线
与直线![]() 相切,且圆
相切,且圆![]() 的圆心在坐标原点,可以求出圆的方程,假设出
的圆心在坐标原点,可以求出圆的方程,假设出![]() 点和
点和![]() 点的坐标,利用
点的坐标,利用![]() ,可以求出
,可以求出![]() 点和
点和![]() 点坐标关系,用
点坐标关系,用![]() 点坐标表示出
点坐标表示出![]() 点坐标,由于点
点坐标,由于点![]() 在圆上,将点
在圆上,将点![]() 坐标代入圆的方程中,可以得出点
坐标代入圆的方程中,可以得出点![]() 的轨迹;
的轨迹;
(2)由于直线![]() 与直线
与直线![]() 垂直,可以得出直线
垂直,可以得出直线![]() 的斜率,进而可以假设出直线
的斜率,进而可以假设出直线![]() 的方程,联立直线
的方程,联立直线![]() 的方程及椭圆
的方程及椭圆![]() 的方程,利用韦达定理可以表示出线段
的方程,利用韦达定理可以表示出线段![]() 的长,由点到直线的距离可以求出点
的长,由点到直线的距离可以求出点![]() 到
到![]() 的距离,进而可以求出
的距离,进而可以求出![]() 的表达式,利用基本不等式可以求出
的表达式,利用基本不等式可以求出![]() 面积的最大值.
面积的最大值.
试题解析:
(1)设动点![]() ,
,![]() 因为
因为![]() 轴于
轴于![]() ,所以
,所以![]() ,
,
设圆![]() 的方程为
的方程为![]()
由题意得![]() ,
,
所以圆![]() 的程为
的程为![]() .
.
由题意, ![]() ,所以
,所以![]() ,
,
所以,即![]()
将![]()
代入圆![]() ,得动点
,得动点![]() 的轨迹方程
的轨迹方程![]() ,
,
(Ⅱ)由题意设直线l![]() 设直线
设直线![]() 与椭圆交于
与椭圆交于![]()
![]() ,联立方程
,联立方程![]() 得
得![]() ,
,
![]() ,解得
,解得![]() ,
,
![]() ,
,
又因为点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,![]()
![]() .
.
![]() 面积的最大值为
面积的最大值为![]() .
.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】(本小题12分)如图,在海岸线![]() 一侧有一休闲游乐场,游乐场的前一部分边界为曲线段
一侧有一休闲游乐场,游乐场的前一部分边界为曲线段![]() ,该曲线段是函数
,该曲线段是函数![]() ,
,![]() 的图像,图像的最高点为
的图像,图像的最高点为![]() .边界的中间部分为长
.边界的中间部分为长![]() 千米的直线段
千米的直线段![]() ,且
,且![]() .游乐场的后一部分边界是以
.游乐场的后一部分边界是以![]() 为圆心的一段圆弧
为圆心的一段圆弧![]() .
.

(1)求曲线段![]() 的函数表达式;
的函数表达式;
(2)曲线段![]() 上的入口
上的入口![]() 距海岸线
距海岸线![]() 最近距离为
最近距离为![]() 千米,现准备从入口
千米,现准备从入口![]() 修一条笔直的景观路到
修一条笔直的景观路到![]() ,求景观路
,求景观路![]() 长;
长;
(3)如图,在扇形![]() 区域内建一个平行四边形休闲区
区域内建一个平行四边形休闲区![]() ,平行四边形的一边在海岸线
,平行四边形的一边在海岸线![]() 上,一边在半径
上,一边在半径![]() 上,另外一个顶点
上,另外一个顶点![]() 在圆弧
在圆弧![]() 上,且
上,且![]() ,求平行四边形休闲区
,求平行四边形休闲区![]() 面积的最大值及此时
面积的最大值及此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1以直线![]() 所过的定点为一个焦点,且短轴长为4.
所过的定点为一个焦点,且短轴长为4.
(Ⅰ)求椭圆C1的标准方程;
(Ⅱ)已知椭圆C2的中心在原点,焦点在y轴上,且长轴和短轴的长分别是椭圆C1的长轴和短轴的长的倍(>1),过点C(1,0)的直线l与椭圆C2交于A,B两个不同的点,若![]() ,求△OAB的面积取得最大值时直线l的方程.
,求△OAB的面积取得最大值时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来郑州空气污染较为严重,现随机抽取一年(365天)内100天的空气中![]() 指数的监测数据,统计结果如下:
指数的监测数据,统计结果如下:
|
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
记某企业每天由空气污染造成的经济损失为![]() (单位:元),
(单位:元), ![]() 指数为
指数为![]() .当
.当![]() 在区间
在区间![]() 内时对企业没有造成经济损失;当
内时对企业没有造成经济损失;当![]() 在区间
在区间![]() 内时对企业造成经济损失成直线模型(当
内时对企业造成经济损失成直线模型(当![]() 指数为150时造成的经济损失为500元,当
指数为150时造成的经济损失为500元,当![]() 指数为200 时,造成的经济损失为700元);当
指数为200 时,造成的经济损失为700元);当![]() 指数大于300时造成的经济损失为2000元.
指数大于300时造成的经济损失为2000元.
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |
(1)试写出![]() 的表达式;
的表达式;
(2)试估计在本年内随机抽取一天,该天经济损失![]() 大于500元且不超过900元的概率;
大于500元且不超过900元的概率;
(3)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面列联表,并判断是否有![]() 的把握认为郑州市本年度空气重度污染与供暖有关?
的把握认为郑州市本年度空气重度污染与供暖有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,…,第五组,如图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )

A. 6 B. 8
C. 12 D. 18
查看答案和解析>>
科目:高中数学 来源: 题型:
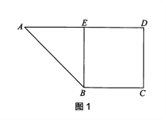
【题目】如图1,梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.将
中点.将![]() 沿
沿![]() 翻折到
翻折到![]() 的位置,使
的位置,使![]() ,如图2.
,如图2.
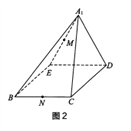
(Ⅰ)求证:平面![]() 与平面
与平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)设![]() 分别为
分别为![]() 和
和![]() 的中点,试比较三棱锥
的中点,试比较三棱锥![]() 和三棱锥
和三棱锥![]() (图中未画出)的体积大小,并说明理由.
(图中未画出)的体积大小,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com