
【题目】已知曲线C1的参数方程为 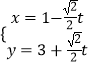 (t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2
(t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2 ![]() sin(θ+
sin(θ+ ![]() ). (Ⅰ)求曲线C1与曲线C2的普通方程;
). (Ⅰ)求曲线C1与曲线C2的普通方程;
(Ⅱ)若点P的坐标为(﹣1,3),且曲线C1与曲线C2交于B,D两点,求|PB||PD|.
【答案】解:(Ⅰ)由曲线C1的参数方程知:曲线C1是过点(﹣1,3)的直线, 相加消去参数t可得:曲线C1的普通方程为x+y﹣2=0.
曲线C2的极坐标方程为ρ=2 ![]() sin(θ+
sin(θ+ ![]() ),
),
展开可得ρ2=2 ![]() ρ(sinθ+cosθ),
ρ(sinθ+cosθ),
利用互化公式可得:曲线C2的直角坐标方程为x2+y2﹣2x﹣2y=0.
(Ⅱ)由判断知:P在直线C1上,
将 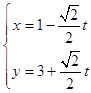 代入方程x2+y2﹣2x﹣2y=0得:
代入方程x2+y2﹣2x﹣2y=0得: ![]() ,
,
设点B,D对应的参数分别为t1 , t2 ,
则|PB|=|t1|,|PD|=|t2|,而t1t2=6,
∴|PB||PD|=|t1||t2|=|t1t2|=6
【解析】(Ⅰ)由曲线C1的参数方程知:曲线C1是过点(﹣1,3)的直线,相加消去参数t可得:曲线C1的普通方程.曲线C2的极坐标方程为ρ=2 ![]() sin(θ+
sin(θ+ ![]() ),展开可得ρ2=2
),展开可得ρ2=2 ![]() ρ(sinθ+cosθ),利用互化公式可得曲线C2的直角坐标方程.(Ⅱ)由判断知:P在直线C1上,将
ρ(sinθ+cosθ),利用互化公式可得曲线C2的直角坐标方程.(Ⅱ)由判断知:P在直线C1上,将  代入曲线C2的方程得:
代入曲线C2的方程得: ![]() ,利用|PB||PD|=|t1||t2|=|t1t2|即可得出.
,利用|PB||PD|=|t1||t2|=|t1t2|即可得出.


科目:高中数学 来源: 题型:
【题目】若数列A:a1 , a2 , …,an(n≥3)中ai∈N*(1≤i≤n)且对任意的2≤k≤n﹣1,ak+1+ak﹣1>2ak恒成立,则称数列A为“U﹣数列”.
(Ⅰ)若数列1,x,y,7为“U﹣数列”,写出所有可能的x,y;
(Ⅱ)若“U﹣数列”A:a1 , a2 , …,an中,a1=1,an=2017,求n的最大值;
(Ⅲ)设n0为给定的偶数,对所有可能的“U﹣数列”A:a1 , a2 , …,an0 , 记M=max{a1 , a2 , …,an0},其中max{x1 , x2 , …,xs}表示x1 , x2 , …,xs这s个数中最大的数,求M的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)的定义域为D={x|x≠0},且满足对于任意x1 , x2∈D,有f(x1x2)=f(x1)+f(x2).
(1)求f(1)的值;
(2)判断f(x)的奇偶性并证明你的结论;
(3)如果f(4)=1,f(x﹣1)<2,且f(x)在(0,+∞)上是增函数,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(1+x)﹣x+ ![]() x2(k≥0). (Ⅰ)当k=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
x2(k≥0). (Ⅰ)当k=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)求f(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)= ![]() 是定义在(﹣1,1)上的奇函数,且f(
是定义在(﹣1,1)上的奇函数,且f( ![]() )=
)= ![]() .
.
(1)确定函数f(x)的解析式;
(2)用定义证明f(x)在(﹣1,1)上是增函数;
(3)解不等式f(t﹣1)+f(t)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() (a>b>0)的上顶点为P(0,1),过E的焦点且垂直长轴的弦长为1.若有一菱形ABCD的顶点A、C在椭圆E上,该菱形对角线BD所在直线的斜率为﹣1.
(a>b>0)的上顶点为P(0,1),过E的焦点且垂直长轴的弦长为1.若有一菱形ABCD的顶点A、C在椭圆E上,该菱形对角线BD所在直线的斜率为﹣1.
(1)求椭圆E的方程;
(2)当直线BD过点(1,0)时,求直线AC的方程;
(3)当∠ABC= ![]() 时,求菱形ABCD面积的最大值.
时,求菱形ABCD面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com