
| an-2n |
| 3n |
| an+1 |
| an |
| an-2n |
| 3n |
| an+1-2n+1 |
| 3n+1 |
| an-2n |
| 3n |
| 3an+3n+1-2n-2n+1 |
| 3n+1 |
| an-2n |
| 3n |
| 9(1-3n-1) |
| 1-3 |
| 9-3n+1 |
| 4 |
| (n-1)•3n+1 |
| 2 |
| (2n-3)•3n+1+9 |
| 4 |
| (2n-3)3n+1+2n+3+1 |
| 4 |
| n•3n+1+2n+1 |
| (n-1)3n+2n |
| 13 |
| 2 |
| 62 |
| 13 |
| 259 |
| 62 |
| an+1 |
| an |
| a2 |
| a1 |
| (n•3n+1+2n+1)•2-13[(n-1)•3n+2n] |
| an•a1 |
| (13-7n)•3n-9.2n |
| an•a1 |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
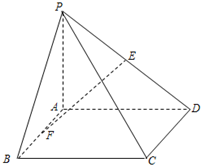 (2012•武昌区模拟)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD,AB=
(2012•武昌区模拟)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD,AB=| 2 |
| PE |
| ED |
| BF |
| FA |
查看答案和解析>>
科目:高中数学 来源: 题型:
| n | 2k |
| s | 2k |
| 1 |
| 2k-1 |
| 1 |
| 2k-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•武昌区模拟)2011年武汉电视台问政直播节日首场内容是“让交通更顺畅”.A、B、C、D四个管理部门的负责人接受问政,分别负责问政A、B、C、D四个管理部门的现场市民代表(每一名代表只参加一个部门的问政)人数的条形图如下.为了了解市民对武汉市实施“让交通更顺畅”几个月来的评价,对每位现场市民都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
(2012•武昌区模拟)2011年武汉电视台问政直播节日首场内容是“让交通更顺畅”.A、B、C、D四个管理部门的负责人接受问政,分别负责问政A、B、C、D四个管理部门的现场市民代表(每一名代表只参加一个部门的问政)人数的条形图如下.为了了解市民对武汉市实施“让交通更顺畅”几个月来的评价,对每位现场市民都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:| 满意 | 一般 | 不满意 | |
| A部门 | 50% | 25% | 25% |
| B部门 | 80% | 0 | 20% |
| C部门 | 50% | 50% | 0 |
| D部门 | 40% | 20% | 40% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com