
分析 本题通过奇函数特征得到函数图象经过原点,且关于原点对称,利用f(x+1)=f(x)+f(1)得到函数类似周期性特征,从而可以画出函数的草图,再利用两个临界状态的研究,得到k的取值范围
解答 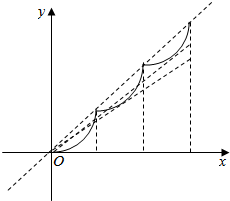 解:∵当0≤x≤1时,f(x)=x2,
解:∵当0≤x≤1时,f(x)=x2,
∴f(1)=1.
∵当x>0时,f(x+1)=f(x)+f(1),
∴f(x+1)=f(x)+1,
∴当x∈[n,n+1],n∈N*时,
f(x+1)=f(x-1)+2=f(x-2)+3=…=f(x-n)+n+1=(x-n)2+n,
∵函数f(x)是定义在R上的奇函数,
∴函数图象经过原点,且关于原点对称.
∵直线y=kx与函数y=f(x)的图象恰有7个不同的公共点,
∴当x>0时,直线y=kx与函数y=f(x)的图象恰有3个不同的公共点,
∴由x>0时f(x)的图象可知:
直线y=kx与函数y=f(x)的图象相切位置在x∈[1,2]时,直线y=kx与函数y=f(x)的图象恰有5个不同的公共点,
直线y=kx与函数y=f(x)的图象相切位置在x∈[2,3]时,直线y=kx与函数y=f(x)的图象恰有9个不同的公共点,
∴直线y=kx与函数y=f(x)的图象位置情况介于上述两种情况之间.
∵当x∈[1,2]时,
由$\left\{\begin{array}{l}{y=kx}\\{y=(x-1)^{2}+1}\end{array}\right.$得:k=2$\sqrt{2}$-2
x2-(k+2)x+2=0,
令△=0,得:k=2$\sqrt{2}$-2.
由$\left\{\begin{array}{l}{y=kx}\\{y=(x-2)^{2}+2}\end{array}\right.$得:
x2-(k+4)x+6=0,
令△=0,得:k=2$\sqrt{6}$-4.
∴k的取值范围为(2$\sqrt{2}$-1,2$\sqrt{6}$-4).
故答案为:(2$\sqrt{2}$-2,2$\sqrt{6}$-4).
点评 本题考查抽象函数及其应用,着重考查函数的零点与方程根的关系,考查函数的对称性、周期性、奇偶性的综合应用,考查转化思想与作图能力,属于难题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | 若$\underset{lim}{x→{x}_{0}}$f(x)和$\underset{lim}{x→{x}_{0}}$g(x)都不存在,则$\underset{lim}{x→{x}_{0}}$[f(x)+g(x)]不存在 | |
| B. | 若$\underset{lim}{x→{x}_{0}}$f(x)和$\underset{lim}{x→{x}_{0}}$g(x)都不存在,则$\underset{lim}{x→{x}_{0}}$[f(x)g(x)]不存在 | |
| C. | $\underset{lim}{x→{x}_{0}}$$\frac{f(x)}{g(x)}$存在,且$\underset{lim}{x→{x}_{0}}$[g(x)]=0,则$\underset{lim}{x→{x}_{0}}$f(x)=0 | |
| D. | 若$\underset{lim}{x→{x}_{0}}$|f(x)|=|A|,$\underset{lim}{x→{x}_{0}}$f(x)=A. |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
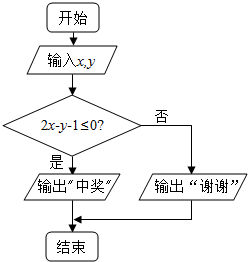 某单位抽奖活动的规则是:代表通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数x,y,并按如图所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,则该代表中奖的概率为( )
某单位抽奖活动的规则是:代表通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数x,y,并按如图所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,则该代表中奖的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com