分析:如图所示,以BC边所在直线为x轴,BC边的垂直平分线为y轴建立直角坐标系(D为BC边的中点).由外接圆的性质可得∠BOD=∠COD=∠BAC.由
cosA=,不妨设外接圆的半径R=3.则OA=OB=OC=3.可得B,C,O的坐标,设A(m,n).则△ABC外接圆的方程为:x
2+(y-1)
2=9.(*)利用向量相等
=α+β,可得
| | -m=α(-2-m)+β(2-m) | | 1-n=-αn-βn |
| |
,又α+β≠1时,否则
=α,由图可知是不可能的.可化为
,代入(*)可得
+=9,化为18(α+β)=9+32αβ,利用重要不等式可得
18(α+β)≤9+32()2,化为8(α+β)
2-18(α+β)+9≥0,即可解出.
解答:解:如图所示,以BC边所在直线为x轴,BC边的垂直平分线为y轴建立直角坐标系(D为BC边的中点).
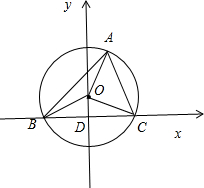
由外接圆的性质可得∠BOD=∠COD=∠BAC.
由
cosA=,不妨设外接圆的半径R=3.则OA=OB=OC=3.
∵
cos∠COD==,∴OD=1.
DC==2.
∴B
(-2,0),C
(2,0),O(0,1),A(m,n).
则△ABC外接圆的方程为:x
2+(y-1)
2=9.(*)
∵
=α+β,
∴(-m,1-n)=
α(-2-m,-n)+β(2-m,-n),
∴
| | -m=α(-2-m)+β(2-m) | | 1-n=-αn-βn |
| |
,
∵α+β≠1时,否则
=α,由图可知是不可能的.
∴可化为
,代入(*)可得
+=9,
化为18(α+β)=9+32αβ,
利用重要不等式可得
18(α+β)≤9+32()2,
化为8(α+β)
2-18(α+β)+9≥0,
解得
α+β≤或
α+β≥.
又α+β<1,故
α+β≥应舍去.
∴
α+β≤,
故α+β的最大值为
.
故选D.
点评:本题考查了通过建立直角坐标系解决向量的有关运算、圆的标准方程、基本不等式的性质、一元二次不等式的解法、三角形的外接圆的性质、余弦函数等基础知识与基本技能方法,属于难题.



