
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)设![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(2)若函数![]() 在
在![]() 内存在零点,求
内存在零点,求![]() 的范围.
的范围.
【答案】(1)见解析;(2)![]() 的取值范围是
的取值范围是![]() .
.
【解析】试题分析:(1)求导可以得到![]() ,分
,分![]() 三种情况讨论导数的符号.(2)计算可以得到
三种情况讨论导数的符号.(2)计算可以得到![]() ,其导数为
,其导数为![]() ,我们需要讨论
,我们需要讨论![]() 的符号,故需再构建新函数
的符号,故需再构建新函数![]() ,其导数为
,其导数为 ,结合原函数
,结合原函数![]() 的形式和
的形式和![]() 的形式,我们发现当
的形式,我们发现当![]() 时
时![]() 恒成立;当
恒成立;当![]() 时,
时, ![]() 在
在![]() 上有极小值点
上有极小值点![]() ,结合
,结合 可知
可知![]() 在
在![]() 上有零点;当
上有零点;当![]() 时,
时, ![]() 恒成立,结合
恒成立,结合![]() 可知,
可知, ![]() 在
在![]() 上也是恒成立的,故而
上也是恒成立的,故而![]() 在
在![]() 上递增
上递增![]() 恒成立.
恒成立.
解析:(1)定义域![]()
故![]() 则
则 ![]()
若![]() ,则
,则 ![]() 在
在 ![]() 上单调递减;
上单调递减;
若![]() ,则
,则 ![]() .
.
(i) 当 ![]() 时,则
时,则 ![]() ,因此在
,因此在![]() 上恒有
上恒有 ![]() ,即
,即 ![]() 在
在![]() 上单调递减;
上单调递减;
(ii)当![]() 时,
时, ![]() ,因而在
,因而在![]() 上有
上有![]() ,在
,在![]() 上有
上有![]() ;因此
;因此 ![]() 在
在 ![]() 上单调递减,在
上单调递减,在![]() 单调递增.
单调递增.
(2)设 ![]() ,
,
![]() ,设
,设![]() ,
,
则  .
.
先证明一个命题:当![]() 时,
时, ![]() .令
.令![]() ,
, ![]() ,故
,故![]() 在
在![]() 上是减函数,从而当
上是减函数,从而当![]() 时,
时, ![]() ,故命题成立.
,故命题成立.
若![]() ,由
,由 ![]() 可知,
可知, ![]() .
.![]() ,故
,故 ![]() ,对任意
,对任意![]() 都成立,故
都成立,故 ![]() 在
在![]() 上无零点,因此
上无零点,因此![]() .
.
(ii)当![]() ,考察函数
,考察函数 ![]() ,由于
,由于 ![]() 在
在 ![]() 上必存在零点.设
上必存在零点.设![]() 在
在 ![]() 的第一个零点为
的第一个零点为![]() ,则当
,则当![]() 时,
时, ![]() ,故
,故 ![]() 在
在 ![]() 上为减函数,又
上为减函数,又 ![]() ,
,
所以当 ![]() 时,
时, ![]() ,从而
,从而 ![]() 在
在 ![]() 上单调递减,故在
上单调递减,故在 ![]() 上恒有
上恒有 ![]() 。即
。即 ![]() ,注意到
,注意到 ![]() ,因此
,因此![]() ,令
,令![]() 时,则有
时,则有![]() ,由零点存在定理可知函数
,由零点存在定理可知函数 ![]() 在
在  上有零点,符合题意.
上有零点,符合题意.
(iii)若![]() ,则由
,则由 ![]() 可知,
可知, ![]() 恒成立,从而
恒成立,从而 ![]() 在
在 ![]() 上单调递增,也即
上单调递增,也即 ![]() 在
在![]() 上单调递增,因此
上单调递增,因此![]() ,即
,即![]() 在
在 ![]() 上单调递增,从而
上单调递增,从而![]() 恒成立,故方程
恒成立,故方程 ![]() 在
在 ![]() 上无解.
上无解.
综上可知, ![]() 的取值范围是
的取值范围是 ![]() .
.


科目:高中数学 来源: 题型:
【题目】全集![]() ,非空集合
,非空集合![]() ,且
,且![]() 中的点在平面直角坐标系
中的点在平面直角坐标系![]() 内形成的图形关于
内形成的图形关于![]() 轴、
轴、![]() 轴和直线
轴和直线![]() 均对称.下列命题:
均对称.下列命题:
①若![]() ,则
,则![]() ;
;
②若![]() ,则
,则![]() 中至少有8个元素;
中至少有8个元素;
③若![]() ,则
,则![]() 中元素的个数一定为偶数;
中元素的个数一定为偶数;
④若![]() ,则
,则![]() .
.
其中正确命题的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上的偶函数,且f(2+x)=f(2-x),当x∈[-2,0)时,f(x)=![]() -1,若关于x的方程f(x)-loga(x+2)=0(a>0且a≠1)在区间(-2,6)内恰有4个不等的实数根,则实数a的取值范围是( )
-1,若关于x的方程f(x)-loga(x+2)=0(a>0且a≠1)在区间(-2,6)内恰有4个不等的实数根,则实数a的取值范围是( )
A. ![]() B. (1,4)
B. (1,4)
C. (1,8) D. (8,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元.设该公司一年内共生产该品牌服装x千件并全部销售完,每千件的销售收入为![]() 万元,且
万元,且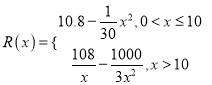 .
.
(1)写出年利润W(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得利润最大?(注:年利润=年销售收入﹣年总成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,取相同的单位长度建立极坐标系,已知曲线
轴正半轴为极轴,取相同的单位长度建立极坐标系,已知曲线![]() ,直线
,直线![]() .
.
(1)将曲线![]() 上所有点的横坐标、纵坐标分别伸长为原来的2倍、
上所有点的横坐标、纵坐标分别伸长为原来的2倍、![]() 倍后得到曲线
倍后得到曲线![]() ,请写出直线
,请写出直线![]() ,和曲线
,和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 经过点
经过点![]() 且
且![]() ,
, ![]() 与曲线
与曲线![]() 交于点
交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018届辽宁省凌源市高三上学期期末】随着科技的发展,手机成为人们日常生活中必不可少的通信工具,现在的中学生几乎都拥有了属于自己的手机.为了调查某地区高中生一周内使用手机的频率,某机构随机抽查了该地区100名高中生某一周内使用手机的时间(单位:小时),所取样本数据分组区间为![]() ,由此得到如图所示的频率分布直方图.
,由此得到如图所示的频率分布直方图.

(1)求![]() 的值并估计该地区高中生一周使用手机时间的平均值;
的值并估计该地区高中生一周使用手机时间的平均值;
(2)从使用手机时间在![]() 的四组学生中,用分层抽样方法抽取13人,则每组各应抽取多少人?
的四组学生中,用分层抽样方法抽取13人,则每组各应抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如今我们的互联网生活日益丰富,除了可以很方便地网购,网上叫外卖也开始成为不少人日常生活中不可或缺的一部分,为了解网络外卖在![]() 市的普及情况,
市的普及情况, ![]() 市某调查机构借助网络进行了关于网络外卖的问卷调查,并从参与调查的网民中抽取了200人进行抽样分析,得到表格(单位:人).
市某调查机构借助网络进行了关于网络外卖的问卷调查,并从参与调查的网民中抽取了200人进行抽样分析,得到表格(单位:人).

(1)根据表中数据,能否在犯错误的概率不超过0.15的前提下认为![]() 市使用网络外卖的情况与性别有关?
市使用网络外卖的情况与性别有关?
(2)①现从所抽取的女网民中利用分层抽样的方法再抽取5人,再从这5人中随机选出了3人赠送外卖优惠券,求选出的3人中至少有2人经常使用网络外卖的概率;
②将频率视为概率,从![]() 市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用网络外卖的人数为
市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用网络外卖的人数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式:  ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】狄利克雷函数是高等数学中的一个典型函数,若![]() ,则称
,则称![]() 为狄利克雷函数.对于狄利克雷函数
为狄利克雷函数.对于狄利克雷函数![]() ,给出下面4个命题:①对任意
,给出下面4个命题:①对任意![]() ,都有
,都有![]() ;②对任意
;②对任意![]() ,都有
,都有![]() ;③对任意
;③对任意![]() ,都有
,都有![]() ,
, ![]() ;④对任意
;④对任意![]() ,都有
,都有![]() .其中所有真命题的序号是( )
.其中所有真命题的序号是( )
A. ①④ B. ②③ C. ①②③ D. ①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com