
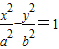 (a>0,b>0)其右准线交x轴于点A,双曲线虚轴的下端点为B,过双曲线的右焦点F(c,0)作垂直于x轴的直线交双曲线于点P,若点D满足:
(a>0,b>0)其右准线交x轴于点A,双曲线虚轴的下端点为B,过双曲线的右焦点F(c,0)作垂直于x轴的直线交双曲线于点P,若点D满足: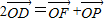 (O为原点)且
(O为原点)且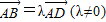
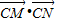 为常数,若存在,求出C点的坐标,若不存在,请说明理由.
为常数,若存在,求出C点的坐标,若不存在,请说明理由.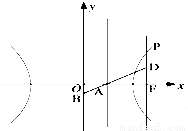
 求出D的坐标,再根据
求出D的坐标,再根据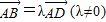 即可求出a和b之间的关系,进而求出曲线的离心率;
即可求出a和b之间的关系,进而求出曲线的离心率; 为常数u,设MN的方程为y=kx-1;联立直线方程与双曲线方程求出M,N的坐标与k之间的关系以及k所满足的范围;再求出
为常数u,设MN的方程为y=kx-1;联立直线方程与双曲线方程求出M,N的坐标与k之间的关系以及k所满足的范围;再求出 的值结合
的值结合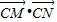 为常数即可得出结论.
为常数即可得出结论. ,P(c,
,P(c,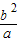 )
)
 ,
,
 ?,
?, 得a=2b
得a=2b (4分)?
(4分)?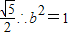
 ①(5分)
①(5分) 为常数u,设MN的方程为y=kx-1 ②(6分)
为常数u,设MN的方程为y=kx-1 ②(6分)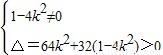 得
得
 ?(8分)
?(8分) ?
? ?
?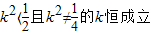 ,
, 解得n=4,u=17
解得n=4,u=17 为常数17 (14分)
为常数17 (14分)

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省衡阳八中高三(下)第九次月考数学试卷(理科)(解析版) 题型:选择题
 ,A,C分别是虚轴的上、下顶点,B是左顶点,F为左焦点,直线AB与FC相交于点D,则∠BDF的余弦值是( )
,A,C分别是虚轴的上、下顶点,B是左顶点,F为左焦点,直线AB与FC相交于点D,则∠BDF的余弦值是( )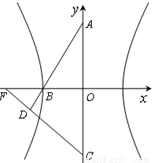



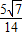
查看答案和解析>>
科目:高中数学 来源:2008-2009学年重庆市西南师大附中高三(下)4月月考数学试卷(理科)(解析版) 题型:解答题
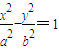 (a>0,b>0)其右准线交x轴于点A,双曲线虚轴的下端点为B,过双曲线的右焦点F(c,0)作垂直于x轴的直线交双曲线于点P,若点D满足:
(a>0,b>0)其右准线交x轴于点A,双曲线虚轴的下端点为B,过双曲线的右焦点F(c,0)作垂直于x轴的直线交双曲线于点P,若点D满足: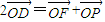 (O为原点)且
(O为原点)且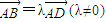
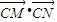 为常数,若存在,求出C点的坐标,若不存在,请说明理由.
为常数,若存在,求出C点的坐标,若不存在,请说明理由.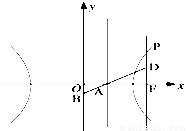
查看答案和解析>>
科目:高中数学 来源:期末题 题型:单选题
 ,A,C分别是虚轴的上、下顶点,B是左顶点,F为左焦点,直线AB与FC相交于点D,则∠BDF的余弦值是
,A,C分别是虚轴的上、下顶点,B是左顶点,F为左焦点,直线AB与FC相交于点D,则∠BDF的余弦值是




查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com