
已知函数 ,
, ,
, ,其中
,其中 ,且
,且 .
.
⑴当 时,求函数
时,求函数 的最大值;
的最大值;
⑵求函数 的单调区间;
的单调区间;
⑶设函数 若对任意给定的非零实数
若对任意给定的非零实数 ,存在非零实数
,存在非零实数 (
( ),使得
),使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
⑴-1; ⑵详见解析; ⑶
解析试题分析:⑴令g′(x)=0求出根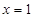 ,判断g′(x)在
,判断g′(x)在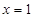 左右两边的符号,得到g(x)在
左右两边的符号,得到g(x)在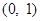 上单调递增,在
上单调递增,在 上单调递减,可知g(x)最大值为g(1),并求出最值;
上单调递减,可知g(x)最大值为g(1),并求出最值;
⑵解不等式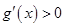 得出函数
得出函数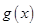 的单调增区间,导数小于零求出单调递减区间,注意单调区间与定义域取交集;
的单调增区间,导数小于零求出单调递减区间,注意单调区间与定义域取交集;
⑶不等式恒成立就是求函数的最值,注意对参数的讨论.
试题解析:⑴当 时,
时, ∴
∴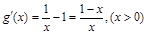
令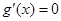 ,则
,则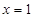 , ∴
, ∴ 在
在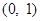 上单调递增,在
上单调递增,在 上单调递减
上单调递减
∴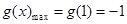 (4分)
(4分)
⑵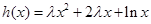 ,
, ,(
,(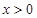 )
)
∴当 时,
时,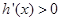 ,∴函数
,∴函数 的增区间为
的增区间为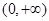 ,
,
当 时,
时,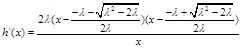 ,
,
当 时,
时,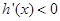 ,函数
,函数 是减函数;当
是减函数;当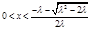 时,
时,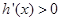 ,函数
,函数 是增函数.
是增函数.
综上得,当 时,
时, 的增区间为
的增区间为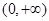 ;
;
当 时,
时, 的增区间为
的增区间为 ,减区间为
,减区间为 (10分)
(10分)
⑶当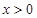 ,
,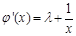 在
在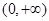 上是减函数,此时
上是减函数,此时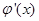 的取值集合
的取值集合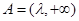 ;
;
当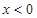 时,
时,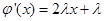 ,
,
若 时,
时,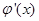 在
在 上是增函数,此时
上是增函数,此时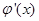 的取值集合
的取值集合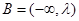 ;
;
若 时,
时,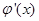 在
在 上是减函数,此时
上是减函数,此时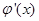 的取值集合
的取值集合 .
.
对任意给定的非零实数 ,
,
①当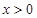 时,∵
时,∵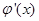 在
在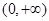 上是减函数,则在
上是减函数,则在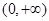 上不存在实数
上不存在实数 (
( ),使得
),使得 ,则
,则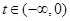 ,要在
,要在 上存在非零实数
上存在非零实数 (
( ),使得
),使得 成立,必定有
成立,必定有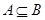 ,∴
,∴ ;
;
②当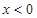 时,
时,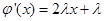 在
在 时是单调函数,则
时是单调函数,则

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:解答题
定义在 上的函数
上的函数 同时满足以下条件:
同时满足以下条件:
① 在(0,1)上是减函数,在(1,+∞)上是增函数;
在(0,1)上是减函数,在(1,+∞)上是增函数;
② 是偶函数;
是偶函数;
③ 在x=0处的切线与直线
在x=0处的切线与直线 y=x+2垂直.
y=x+2垂直.
(1)求函数 =
= 的解析式;
的解析式;
(2)设g(x)= ,若存在实数x∈[1,e],使
,若存在实数x∈[1,e],使 <
< ,求实数m的取值范围.
,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两地相距1000 ,货车从甲地匀速行驶到乙地,速度不得超过80
,货车从甲地匀速行驶到乙地,速度不得超过80 ,已知货车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本是速度平方的
,已知货车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本是速度平方的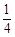 倍,固定成本为a元.
倍,固定成本为a元.
(1)将全程运输成本y(元)表示为速度v( )的函数,并指出这个函数的定义域;
)的函数,并指出这个函数的定义域;
(2)为了使全程运输成本最小,货车应以多大的速度行驶?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com