练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设函数.

    （1）当a=2时，判断函数在定义域内的单调性；

    （2）当时，恒成立，求实数a的取值范围.

    【答案】（1） 在上是增函数;（2） .

    【解析】

    试题分析：（1）首先求函数的导数，令，并且注意函数的定义域，再求函数导数的导数，分和讨论的正负，同时得到函数的单调性，求得的最小值为0，即恒成立，得到函数的单调性；（2）由（1）可得当时，不等式恒成立，当时，记，根据导数求函数的最值，证明不等式不恒成立.

    试题解析：（1）的定义域为，，

    记，则，

    当x>0时，，此时，

    当-1<x<0时，，此时，

    所以在（-1,0）上递减，在上递增，∴，

    ∴f（x）在上是增函数.

    （2），由（1）知在上递增，所以当时，，

    所以f（x）在上递增，故恒成立.

    当a>2时，记，则，

    当x>1时，，

    显然当时，，从而在上单调递增.

    又，则存在，使得.

    所以在上递减，所以当时，，

    即f（x）<cosx，不符合题意.

    综上，实数a的取值范围是.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】中，，，于点，于点.

    （1）如图1，作的角平分线交于点，连接.求证：；

    （2）如图2，连接，点与点关于直线对称，连接、.

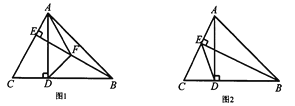
    ①依据题意补全图形；

    ②用等式表示线段、、之间的数量关系，并加以证明.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下面是一段演绎推理：

    大前提：如果直线平行于平面，则这条直线平行于平面内的所有直线；

    小前提：已知直线b∥平面α，直线a平面α；

    结论：所以直线b∥直线a.在这个推理中(　　)

    A. 大前提正确，结论错误 B. 大前提错误，结论错误

    C. 大、小前提正确，只有结论错误 D. 小前提与结论都是错误的

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，正方体中，棱长，过点的平面与正方体的面相交，交线围成一个正三角形．

    （1）在图中画出这个正三角形（不必说明画法和理由）；

    （2）平面将该正方体截成两个几何体，求体积较大的几何体的体积和表面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列表述正确的是（ ）

    ①归纳推理是由部分到整体的推理； ②归纳推理是由一般到一般的推理；

    ③演绎推理是由一般到特殊的推理； ④类比推理是由特殊到一般的推理；

    ⑤类比推理是由特殊到特殊的推理.

    A. ①②③ B. ②③④ C. ②④⑤ D. ①③⑤

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱柱中，底面ABCD是菱形，且.

    （1）求证：平面平面；

    （2）若，求二面角的大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我们把平面几何里相似的概念推广到空间：如果两个几何体大小不一定相等，但形状完全相同，就称它们是相似体，给出下面的几何体：

    ①两个球体；②两个长方体；③两个正四面体；④两个正三棱柱；⑤两个正四棱锥，则一定是相似体的个数是（ ）

    A. 4 B. 2 C. 3 D. 1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了比较两种治疗失眠症的药（分别称为A药，B药）的疗效，随机地选取20位患者服用A药，20位患者服用B药，这40位患者在服用一段时间后，记录他们日平均增加的睡眠时间（单位：h）．试验的观测结果如下：

    服用A药的20位患者日平均增加的睡眠时间：

    0.6

    1.2

    2.7

    1.5

    2.8

    1.8

    2.2

    2.3

    3.2

    3.5

    2.5

    2.6

    1.2

    2.7

    1.5

    2.9

    3.0

    3.1

    2.3

    2.4

    服用B药的20位患者日平均增加的睡眠时间：

    3.2

    1.7

    1.9

    0.8

    0.9

    2.4

    1.2

    2.6

    1.3

    1.4

    1.6

    0.5

    1.8

    0.6

    2.1

    1.1

    2.5

    1.2

    2.7

    0.5

    （1） 分别计算两组数据的平均数，从计算结果看，哪种药的疗效更好？

    （2） 根据两组数据完成下面茎叶图，从茎叶图看，哪种药的疗效更好？

    A药

    B药

    0.

    1.

    2.

    3.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中.

    （1）当时，求的单调递增区间；

    （2）若在区间上的最小值为8，求的值.

    查看答案和解析>>

    同步练习册答案