设集合A={x|2≤x＜4}.B={x|3x-7≥8-2x}．(1)求集合B.A∪B, (2)求(∁RA)∩B.A∪(∁RB)．题目和参考答案——青夏教育精英家教网—

19．设集合A={x|2≤x＜4}，B={x|3x-7≥8-2x}．
（1）求集合B，A∪B；
（2）求（∁_RA）∩B，A∪（∁_RB）．

分析（1）化简集合B，根据并集的定义写出A∪B即可；
（2）根据补集、交集和并集的定义直接计算即可．

解答解：（1）集合B={x|3x-7≥8-2x}={x|x≥3}；
又集合A={x|2≤x＜4}，
所以A∪B={x|x≥2}；
（2）因为∁_RA={x|x＜2x≥4}，
所以（C_RA）∩B={x|x≥4}；
又∁_RB={x|x＜3}，
所以A∪（C_RB）={x|x＜4}．

点评本题考查了集合的化简与基本运算问题，是基础题目．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

2．$\frac{1}{a}＞-1$是a＜-1成立的（　　）

	A．	充分不必要条件		B．	必要不充分条件
	C．	充要条件		D．	既不充分也不必要条件

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

10．美国篮球职业联赛（NBA）某赛季的总决赛在湖人队与活塞队之间进行，比赛采取七局四胜制．即若有一队胜四场，则此队获胜且比赛结束．因两对实力非常接近，在每场比赛中每队获胜是等可能的，据资料统计，每场比赛组织者可获门票及广告收入1000万美元．求在这次总决赛过程中．
（1）比赛5局湖人队取胜的概率；
（2）比赛组织者获得门票及广告收入ξ（万美元）的概率分布列及数学期望Eξ．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

7．设i是虚数单位，如果复数$\frac{a-i}{2+i}$的实部与虚部是互为相反数，那么实数a的值为（　　）

A．

$\frac{1}{3}$

B．

$-\frac{1}{3}$

C．

D．

-3

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

14．

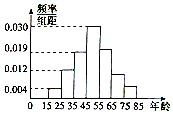某购物中心为了了解顾客使用新推出的某购物卡的顾客的年龄分布情况，随机调查了100位到购物中心购物的顾客年龄，并整理后画出频率分布直方图如图所示，年龄落在区间[55，65），[65，75），[75，85]内的频率之比为4：2：1．
（1）求顾客年龄值落在区间[75，85]内的频率；
（2）拟利用分层抽样从年龄在[55，65），[65，75）的顾客中选取6人召开一个座谈会，现从这6人中选出2人，求这两人在不同年龄组的概率．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

4．将函数f（x）=sin2xcos2x+$\sqrt{3}{cos^2}2x-\frac{{\sqrt{3}}}{2}$的图象上所有点纵坐标不变，横坐标伸长到原来的2倍，再向右平行移动$\frac{π}{3}$个单位长度得函数g（x）图象，则以下说法正确的是（　　）

	A．	函数g（x）在区间$[{0，\frac{π}{2}}]$上单调递增		B．	函数f（x）与g（x）的最小正周期均为π
	C．	函数g（x）在区间$[{0，\frac{π}{2}}]$上的最大值为$\frac{{\sqrt{3}}}{2}$		D．	函数g（x）的对称中心为$（{\frac{Kπ}{2}+\frac{π}{6}，0}）$（K∈Z）

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

11．已知关于x的方程k•9^x-3k•3^x+6（k-5）=0，x∈[0，2]；分别求满足下列条件的实数k的取值范围：（1）有解；（2）有唯一解；（3）有两个解．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

8．设α={-1，1，$\frac{1}{2}$}，则使函数y=x^α的定义域为R且为奇函数的所有α的值为1．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

9．已知x，y满足约束条件$\left\{\begin{array}{l}x+y≤5\\ x-4y≤0\\ x-y+3≥0\end{array}\right.$，则下列目标函数中，在点（4，1）处取得最大值的是（　　）

A．

$z=\frac{1}{5}x-y$

B．