练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，已知四边形ABCD是平行四边形，点P是平面ABCD外一点，M是PC的中点，在DM上取一点G，过G和AP的平面交平面BDM于GH，H在BD上．

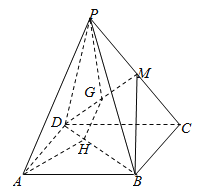
    （1）求证平面BDM．

    （2）若G为DM中点，求证：．

    【答案】（1）证明见解析；（2）证明见解析.

    【解析】

    （1）连AC交BD于O，连接OM，由中位线定理可得，再根据线面平行的判定定理即可证出平面BDM；

    （2）根据线面平行的性质定理可知， ，又由（1）知，所以，

    再根据中位线定理即可得到．

    （1）连AC交BD于O，连接OM，

    因为四边形ABCD是平行四边形，所以O是AC的中点．

    又M是PC的中点，所以，

    又平面BDM，平面BDM

    所以，平面BDM．

    （2）因为经过AP与点G的平面交平面BDM于GH，

    平面BDM，平面APGH，平面平面，

    所以，由线面平行的性质定理得．

    又∵，∴

    又∵G为DM中点，

    ∴，，∴．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在直角梯形ABCD中，，，，，E为AB的中点.将沿CE折起，使点B到达点F的位置，且平面CEF与平面ADCE所成的二面角为.

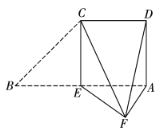
    （1）求证：平面平面AEF；

    （2）求直线DF与平面CEF所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知,且.

    （1）求的值；

    （2）证明: 存在唯一的极小值点,且.

    (参考数据: )

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从分别写有数字1，2，3，4，5的5张卡片中随机抽取1张，放回后再随机抽取1张，则抽得的第一张卡片上的数字不大于第二张卡片的概率是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，直三棱柱中，，，，，点D，E分别为AB，的中点．

    （1）求证：平面平面；

    （2）求异面直线与所成角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校高一年级开设了丰富多彩的校本课程，现从甲、乙两个班随机抽取了5名学生校本课程的学分，统计如下表．

    甲

    8

    11

    14

    15

    22

    乙

    6

    7

    10

    23

    24

    用分别表示甲、乙两班抽取的5名学生学分的方差，计算两个班学分的方差．得______，并由此可判断成绩更稳定的班级是______班．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知的定义域为，，使得不等式成立，关于的不等式的解集记为.

    （1）若为真，求实数的取值集合；

    （2）在（1）的条件下，若是的充分不必要条件，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从6名男医生和3名女医生中选出5人组成一个医疗小组，请解答下列问题：

    （1）如果这个医疗小组中男女医生都不能少于2人，共有多少种不同的建组方案？（用数字作答）

    （2）男医生甲要担任医疗小组组长，所以必选，而且医疗小组必须男女医生都有，共有多少种不同的建组方案？

    （3）男医生甲与女医生乙不被同时选中的概率.（化成最简分数）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线恒过定点.

    （Ⅰ）若直线经过点且与直线垂直，求直线的方程；

    （Ⅱ）若直线经过点且坐标原点到直线的距离等于3，求直线的方程.

    查看答案和解析>>

    同步练习册答案