
【题目】已知点![]() 在抛物线
在抛物线![]() 上,点
上,点![]() 是抛物线
是抛物线![]() 的焦点,线段
的焦点,线段![]() 的中点为
的中点为![]() .
.
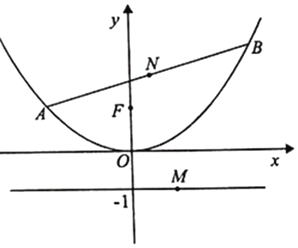
(1)若点![]() 的坐标为
的坐标为![]() ,且
,且![]() 是
是![]() 的垂心,求直线
的垂心,求直线![]() 的方程;
的方程;
(2)若点![]() 是直线
是直线![]() 上的动点,且
上的动点,且![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)2.
;(2)2.
【解析】
(1)求得抛物线的焦点和准线方程,求得![]() 的斜率,可得
的斜率,可得![]() 的斜率,设
的斜率,设![]() 的方程,联立抛物线方程,运用判别式大于0和韦达定理,运用两直线垂直的条件,可得
的方程,联立抛物线方程,运用判别式大于0和韦达定理,运用两直线垂直的条件,可得![]() 的方程,求得
的方程,求得![]() 的值,即可得到所求直线方程;
的值,即可得到所求直线方程;
(2)显然![]() 最小,必须
最小,必须![]() 垂直于直线
垂直于直线![]() ,分别过
,分别过![]() ,
,![]() 作
作![]() ,
,![]() 垂直直线
垂直直线![]() ,垂足为
,垂足为![]() ,
,![]() ,运用梯形的中位线定理,以及三点共线取得最小值,即可得到所求最小值.
,运用梯形的中位线定理,以及三点共线取得最小值,即可得到所求最小值.
(1)![]() 的焦点
的焦点![]() ,准线方程为
,准线方程为![]() ,
,
![]() ,
,![]() 为
为![]() 的垂心,可得
的垂心,可得![]() ,即有
,即有![]() ,
,
设![]() 的方程为
的方程为![]() ,代入抛物线方程可得:
,代入抛物线方程可得:
![]() ,可得
,可得![]() ,
,
由![]() ,可得
,可得 ,
,
![]() ,
,
化简可得![]() ,
,
即为![]() ,解得
,解得![]() ,
,
由![]() ,可得
,可得![]() ,
,
则![]() 的方程为
的方程为![]() ;
;
(2)显然![]() 最小,必须
最小,必须![]() 垂直于直线
垂直于直线![]() ,
,
分别过![]() 作
作![]() 垂直直线
垂直直线![]() ,垂足为
,垂足为![]() ,
,
![]() ,
,
等号成立当且仅当![]() 三点共线,且
三点共线,且![]() 轴,
轴,
所以![]() 的最小值为2.
的最小值为2.



 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:
【题目】中央电视台为了解一档诗歌类节目的收视情况,抽查东西两部各5个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示:
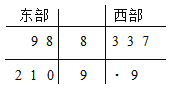
其中一个数字被污损;
(1)求东部各城市观看该节目观众平均人数超过西部各城市观看该节目观众平均人数的概率;
(2)随着节目的播出,极大激发了观众对诗歌知识的学习积累热情,从中获益匪浅.现从观看该节目的观众中随机统计了4位观众的周均学习诗歌知识的时间(单位:小时)与年龄(单位:岁),并制作了对照表(如下表所示):

由表中数据,试求线性回归方程![]() ,并预测年龄在60岁的观众周均学习诗歌知识的时间.
,并预测年龄在60岁的观众周均学习诗歌知识的时间.
参考公式: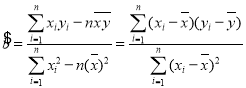 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个口袋有m个白球,n个黑球(m,n![]()
![]() ,n
,n![]() 2),这些球除颜色外全部相同。现将口袋中的球随机的逐个取出,并放入如图所示的编号为1,2,3,……,m+n的抽屉内,其中第k次取球放入编号为k的抽屉(k=1,2,3,……,m+n).
2),这些球除颜色外全部相同。现将口袋中的球随机的逐个取出,并放入如图所示的编号为1,2,3,……,m+n的抽屉内,其中第k次取球放入编号为k的抽屉(k=1,2,3,……,m+n).
![]()
(1)试求编号为2的抽屉内放的是黑球的概率p;
(2)随机变量x表示最后一个取出的黑球所在抽屉编号的倒数,E(x)是x的数学期望,证明 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司有![]() 四辆汽车,其中
四辆汽车,其中![]() 车的车牌尾号为0,
车的车牌尾号为0,![]() 两辆车的车牌尾号为6,
两辆车的车牌尾号为6,![]() 车的车牌尾号为5,已知在非限行日,每辆车都有可能出车或不出车.已知
车的车牌尾号为5,已知在非限行日,每辆车都有可能出车或不出车.已知![]() 两辆汽车每天出车的概率为
两辆汽车每天出车的概率为![]() ,
,![]() 两辆汽车每天出车的概率为
两辆汽车每天出车的概率为![]() ,且四辆汽车是否出车是相互独立的.
,且四辆汽车是否出车是相互独立的.
该公司所在地区汽车限行规定如下:

(1)求该公司在星期四至少有2辆汽车出车的概率;
(2)设![]() 表示该公司在星期一和星期二两天出车的车辆数之和,求
表示该公司在星期一和星期二两天出车的车辆数之和,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域是![]() 上的连续函数
上的连续函数![]() 图像的两个端点为
图像的两个端点为![]() 、
、![]() ,
,![]() 是图像
是图像![]() 上任意一点,过点
上任意一点,过点![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() 交线段
交线段![]() 于点
于点![]() (点
(点![]() 与点
与点![]() 可以重合),我们称
可以重合),我们称![]() 的最大值为该函数的“曲径”,下列定义域是
的最大值为该函数的“曲径”,下列定义域是![]() 上的函数中,曲径最小的是( )
上的函数中,曲径最小的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在△ABC中,角A,B,C所对的边分别为a,b,c,其中A为锐角,且asin(B+C)是![]() bcosC与
bcosC与![]() ccosB的等差中项.
ccosB的等差中项.
(1)求角A的大小;
(2)若点D在△ABC的内部,且满足∠CAD=∠ABD![]() ,∠CBD
,∠CBD![]() ,AD=1,求CD的长.
,AD=1,求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com