
【题目】已知函数![]() .
.
(Ⅰ)若函数![]() 图象在点
图象在点![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)求函数![]() 的极值;
的极值;
(Ⅲ)若![]() ,
,![]() ,且对任意的
,且对任意的![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】(Ⅰ)利用导数的几何意义,先对![]() 进行求导,再利用
进行求导,再利用![]() ,可求出
,可求出![]() 的值;(Ⅱ)求出
的值;(Ⅱ)求出![]() 的表达式,再分别对
的表达式,再分别对![]() 两种进行讨论,可得到函数
两种进行讨论,可得到函数![]() 的极值;(Ⅲ)函数恒成立问题,两种思路,一种是
的极值;(Ⅲ)函数恒成立问题,两种思路,一种是![]() ,另一种是用参变分离的方法求解.
,另一种是用参变分离的方法求解.
试题分析:(Ⅰ)![]() ,∴
,∴![]() .
.
函数![]() 图象在点
图象在点![]() 处的切线方程为
处的切线方程为![]() ∴
∴![]()
(Ⅱ)由题意可知,函数![]() 的定义域为
的定义域为![]() ,
,
![]()
当![]() 时,
时,![]() ,
,![]() ,
,![]() 为增函数
为增函数![]() ,
,![]() ,
,![]() 为减函数,所以
为减函数,所以![]() ,
,![]() .
.
当![]() 时,
时,![]() ,
,![]() ,
,![]() 为减函数,
为减函数,![]() ,
,![]() ,
,![]() 为增函数,所以
为增函数,所以![]() ,
,![]() .
.
(Ⅲ)“对任意的![]() ,
,![]() 恒成立”等价于“当
恒成立”等价于“当![]() 时,对任意的
时,对任意的![]() ,
,![]() 成立”,当
成立”,当![]() 时,由(Ⅱ)可知,函数
时,由(Ⅱ)可知,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,而
上单调递减,而![]() ,所以
,所以![]() 的最小值为
的最小值为![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,显然不满足
,显然不满足![]() ,
,
当![]() 时,令
时,令![]() 得,
得,![]() ,
,![]() ,
,
(ⅰ)当![]() ,即
,即![]() 时,在
时,在![]() 上
上![]() ,所以
,所以![]() 在
在![]() 单调递增,所以
单调递增,所以![]() ,只需
,只需![]() ,得
,得![]() ,所以
,所以![]() .
.
(ⅱ)当![]() ,即
,即![]() 时,在
时,在![]() ,
,![]() ,
,![]() 单调递增,在
单调递增,在![]() ,
,![]() ,
,![]() 单调递减,所以
单调递减,所以![]() ,
,
只需![]() ,得
,得![]() ,所以
,所以![]() .
.
(ⅲ)当![]() ,即
,即![]() 时,显然在
时,显然在![]() 上
上![]() ,
,![]() 单调递增,
单调递增,![]() ,
,![]() 不成立,………………13分
不成立,………………13分
综上所述,![]() 的取值范围是
的取值范围是![]() .
.
(用分离参数做答酌情给分)


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且acosC+ccosA=2bcosA.
(1)求角A的值;
(2)若![]() ,
, ![]() ,求△ABC的面积S.
,求△ABC的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测验中,有6位同学的平均成绩为75分, 用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:
编号n | 1 | 2 | 3 | 4 | 5 |
成绩xn | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩x6,及这6位同学成绩的标准差s;
(2)从前5位同学中选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
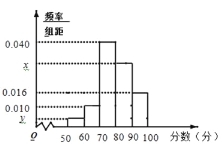
【题目】某重点高中拟把学校打造成新型示范高中,为此制定了学生“七不准”,“一日三省十问”等新的规章制度.新规章制度实施一段时间后,学校就新规章制度随机抽取部分学生进行问卷调查,调查卷共有10个问题,每个问题10分,调查结束后,按分数分成5组: ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并作出频率分布直方图与样本分数的茎叶图(图中仅列出了得分在
,并作出频率分布直方图与样本分数的茎叶图(图中仅列出了得分在![]() ,
,![]() 的数据).
的数据).
(1)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() 、
、![]() 的值;
的值;
(2)在选取的样本中,从分数在70分以下的学生中随机抽取2名学生进行座谈会,求所抽取的2名学生中恰有一人得分在![]() 内的概率.
内的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,且首项a1≠3,an+1=Sn+3n(n∈N*).
(1)求证:数列{Sn-3n}是等比数列;
(2)若{an}为递增数列,求a1的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() :实数
:实数![]() 满足不等式
满足不等式![]() ,
,![]() :函数
:函数![]() 无极值点.
无极值点.
(1)若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围;
的取值范围;
(2)已知. “![]() ”为真命题,并记为
”为真命题,并记为![]() ,且
,且![]() :
:![]() ,若
,若![]() 是
是![]() 的必要不充分条件,求实数
的必要不充分条件,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频数分布表和频率分布直方图,将使用手机时间不低于80分钟的学生称为“手机迷”.

高一学生日均使用手机时间的频数分布表
时间分组 | 频数 |
[0,20) | 12 |
[20,40) | 20 |
[40,60) | 24 |
[60,80) | 18 |
[80,100) | 22 |
[100,120] | 4 |
(1)将频率视为概率,估计哪个年级的学生是“手机迷”的概率大?请说明理由.
(2)在高二的抽查中,已知随机抽到的女生共有55名,其中10名为“手机迷”.根据已知条件完成下面的2×2列联表,并据此资料你有多大的把握认为“手机迷”与性别有关?
非手机迷 | 手机迷 | 合计 | |
男 | |||
女 | |||
合计 |
附:随机变量 (其中
(其中![]() 为样本总量).
为样本总量).
参考数据 |
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】调查表明,高三学生的幸福感与成绩,作业量,人际关系的满意度的指标有极强的相关性,现将这三项的满意度指标分别记为![]() ,并对它们进行量化:0表示不满意,1表示基本满意,2表示满意.再用综合指标
,并对它们进行量化:0表示不满意,1表示基本满意,2表示满意.再用综合指标![]() 的值评定高三学生的幸福感等级:若
的值评定高三学生的幸福感等级:若![]() ,则幸福感为一级;若
,则幸福感为一级;若![]() ,则幸福感为二级;若
,则幸福感为二级;若![]() ,则幸福感为三级. 为了了解目前某高三学生群体的幸福感情况,研究人员随机采访了该群体的10名高三学生,得到如下结果:
,则幸福感为三级. 为了了解目前某高三学生群体的幸福感情况,研究人员随机采访了该群体的10名高三学生,得到如下结果:
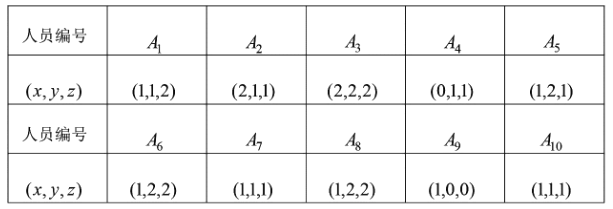
(1)在这10名被采访者中任取两人,求这两人的成绩满意度指标![]() 相同的概率;
相同的概率;
(2)从幸福感等级是一级的被采访者中任取一人,其综合指标为![]() ,从幸福感等级不是一级的被采访者中任取一人,其综合指标为
,从幸福感等级不是一级的被采访者中任取一人,其综合指标为![]() ,记随机变量
,记随机变量![]() ,求
,求![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数,![]() ),且数列
),且数列![]() 是首项为2,公差为2的等差数列.
是首项为2,公差为2的等差数列.
(1)若![]() ,当
,当![]() 时,求数列
时,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(2)设![]() ,如果
,如果![]() 中的每一项恒小于它后面的项,求
中的每一项恒小于它后面的项,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com