
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是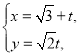 (
(![]() 为参数),曲线
为参数),曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,将曲线
,将曲线![]() 上的点向下平移1个单位,然后横坐标伸长为原来的2倍,纵坐标不变,得到曲线
上的点向下平移1个单位,然后横坐标伸长为原来的2倍,纵坐标不变,得到曲线![]() .
.
(1)求曲线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 和曲线
和曲线![]() 相交于
相交于![]() 两点,求三角形
两点,求三角形![]() 的面积.
的面积.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:![]() 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图.
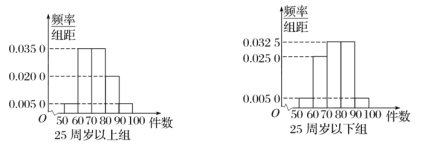
(1)从样本中日平均生产件数不足60的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的概率;
(2)规定日平均生产件数不少于80的为“生产能手”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”?
P( | 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
附: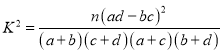
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有9只球,其中标有数字1,2,3,4的小球各2个,标数字5的小球有1个.从袋中任取3个小球,每个小球被取出的可能性都相等,用![]() 表示取出的3个小球上的最大数字.
表示取出的3个小球上的最大数字.
(1)求取出的3个小球上的数字互不相同的概率;
(2)求随机变量![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场统计了2008年到2018十一年间某种生活必需品的年销售额及年销售额增速图,其中条形图表示年(单位:万元),折线图年销售额为年销售额增长率(%).
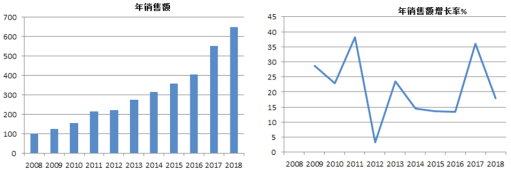
(1)由年销售额图判断,从哪年开始连续三年的年销售额方差最大?(结论不要求证明)
(2)由年销售额增长率图,可以看出2011年销售额增长率是最高的,能否表示当年销售额增长最大?(结论不要求证明)
(3)从2010年至2014年这五年中随机选出两年,求至少有一年年增长率超过20%的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com