练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知正△ABC三个顶点都在半径为2的球面上，球心O到平面ABC的距离为1，点E是线段AB的中点，过点E作球O的截面，则截面面积的最小值是（　　）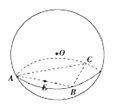

    A.
    B.2π
    C.
    D.3π

    【答案】C
    【解析】解：设正△ABC的中心为O1 ， 连结O1A
    ∵O1是正△ABC的中心，A、B、C三点都在球面上，
    ∴O1O⊥平面ABC，∵球的半径R=2，球心O到平面ABC的距离为1，得O1O=1，
    ∴Rt△O1OA中，O1A= ．
    又∵E为BC的中点，△ABC是等边三角形，∴AE=AO1cos30°= ．
    ∵过E作球O的截面，当截面与OE垂直时，截面圆的半径最小，
    ∴当截面与OE垂直时，截面圆的面积有最小值．
    此时截面圆的半径r= ，
    可得截面面积为S=πr2=π．
    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知、分别是椭圆的左顶点、右焦点，点为椭圆上一动点，当轴时， .

    （1）求椭圆的离心率；

    （2）若椭圆存在点，使得四边形是平行四边形（点在第一象限），求直线与的斜率之积；

    （3）记圆为椭圆的“关联圆”. 若，过点作椭圆的“关联圆”的两条切线，切点为、，直线的横、纵截距分别为、，求证： 为定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图为一简单组合体，其底面ABCD为正方形，PD⊥平面ABCD，EC∥PD，且PD=AD=2EC=2．
    （1）请画出该几何体的三视图；
    （2）求四棱锥B﹣CEPD的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线l过点A（﹣3，4）
    （1）若l与直线y=﹣2x+5平行，求其一般式方程；
    （2）若l与直线y=﹣2x+5垂直，求其一般式方程；
    （3）若l与两个坐标轴的截距之和等于12，求其一般式方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆经过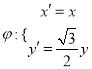变换后得曲线.

    （1）求的方程；

    （2）若为曲线上两点， 为坐标原点，直线的斜率分别为且，求直线被圆截得弦长的最大值及此时直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】命题：已知实数， 满足约束条件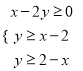，二元一次不等式恒成立，

    命题：设数列的通项公式为，若，使得．

    （1）分别求出使命题， 为真时，实数的取值范围；

    （2）若命题与真假相同，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在平面直角坐标系中，以坐标原点为极点，以轴正半轴为极轴，建立极坐标系，若直线的参数方程为（为参数， 为的倾斜角），曲线的极坐标方程为，射线， ， 与曲线分别交于不同于极点的三点.

    （1）求证： ；

    （2）当时，直线过两点，求与的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

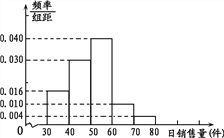
    【题目】某超市计划销售某种产品，先试销该产品天，对这天日销售量进行统计，得到频率分布直方图如图．

    （Ⅰ）若已知销售量低于50的天数为23，求；

    （Ⅱ）厂家对该超市销售这种产品的日返利方案为：每天固定返利45元，另外每销售一件产品，返利3元；频率估计为概率．依此方案，估计日返利额的平均值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x2﹣（a+1）x+1（a∈R）
    （1）若关于x的不等式f（x）＞0的解集为R，求实数a的取值范围；
    （2）若关于x的不等式f（x）≤0的解集为P，集合Q={x|0≤x≤1}，若P∩Q=，求实数a的取值范围．

    查看答案和解析>>

    同步练习册答案